Eje secundario

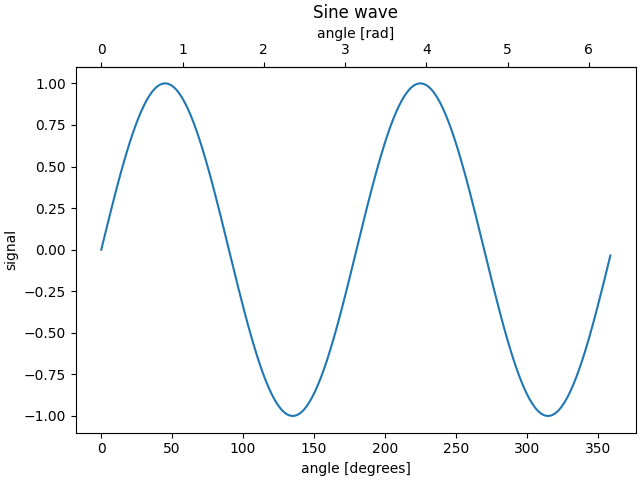
A veces queremos un eje secundario en un gráfico, por ejemplo, para convertir radianes en grados en el mismo gráfico. Podemos hacer esto haciendo que los ejes secundarios con un solo eje sean visibles a través de axes.Axes.secondary_xaxisy axes.Axes.secondary_yaxis. Este eje secundario puede tener una escala diferente a la del eje principal al proporcionar una función de conversión directa e inversa en una tupla al argumento de palabra clave de funciones :

import matplotlib.pyplot as plt
import numpy as np
import datetime
import matplotlib.dates as mdates
from matplotlib.ticker import AutoMinorLocator

fig, ax = plt.subplots(constrained_layout=True)
x = np.arange(0, 360, 1)
y = np.sin(2 * x * np.pi / 180)
ax.plot(x, y)
ax.set_xlabel('angle [degrees]')
ax.set_ylabel('signal')
ax.set_title('Sine wave')


def deg2rad(x):
    return x * np.pi / 180


def rad2deg(x):
    return x * 180 / np.pi


secax = ax.secondary_xaxis('top', functions=(deg2rad, rad2deg))
secax.set_xlabel('angle [rad]')
plt.show()

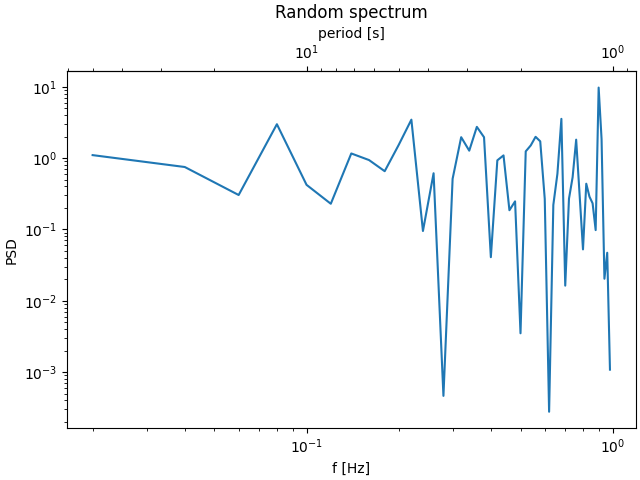
Este es el caso de convertir de número de onda a longitud de onda en una escala logarítmica.

Nota

En este caso, la escala x del padre es logarítmica, por lo que el hijo también se convierte en logarítmico.

fig, ax = plt.subplots(constrained_layout=True)
x = np.arange(0.02, 1, 0.02)
np.random.seed(19680801)
y = np.random.randn(len(x)) ** 2
ax.loglog(x, y)
ax.set_xlabel('f [Hz]')
ax.set_ylabel('PSD')
ax.set_title('Random spectrum')


def one_over(x):
    """Vectorized 1/x, treating x==0 manually"""
    x = np.array(x).astype(float)
    near_zero = np.isclose(x, 0)
    x[near_zero] = np.inf
    x[~near_zero] = 1 / x[~near_zero]
    return x


# the function "1/x" is its own inverse
inverse = one_over


secax = ax.secondary_xaxis('top', functions=(one_over, inverse))
secax.set_xlabel('period [s]')
plt.show()

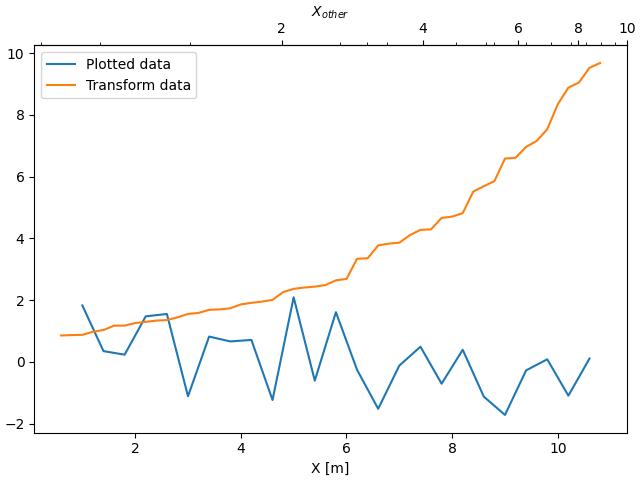
En algún momento queremos relacionar los ejes en una transformación que es ad-hoc de los datos y se deriva empíricamente. En ese caso, podemos configurar las funciones de transformación directa e inversa para que sean interpolaciones lineales de un conjunto de datos al otro.

Nota

Para manejar correctamente los márgenes de datos, las funciones de mapeo ( forwardy inverseen este ejemplo) deben definirse más allá de los límites nominales de la parcela.

En el caso específico de la interpolación lineal numpy numpy.interp, esta condición se puede aplicar arbitrariamente proporcionando argumentos de palabra clave opcionales left , right de modo que los valores fuera del rango de datos se asignen fuera de los límites de la trama.

fig, ax = plt.subplots(constrained_layout=True)
xdata = np.arange(1, 11, 0.4)
ydata = np.random.randn(len(xdata))
ax.plot(xdata, ydata, label='Plotted data')

xold = np.arange(0, 11, 0.2)
# fake data set relating x coordinate to another data-derived coordinate.
# xnew must be monotonic, so we sort...
xnew = np.sort(10 * np.exp(-xold / 4) + np.random.randn(len(xold)) / 3)

ax.plot(xold[3:], xnew[3:], label='Transform data')
ax.set_xlabel('X [m]')
ax.legend()


def forward(x):
    return np.interp(x, xold, xnew)


def inverse(x):
    return np.interp(x, xnew, xold)


secax = ax.secondary_xaxis('top', functions=(forward, inverse))
secax.xaxis.set_minor_locator(AutoMinorLocator())
secax.set_xlabel('$X_{other}$')

plt.show()

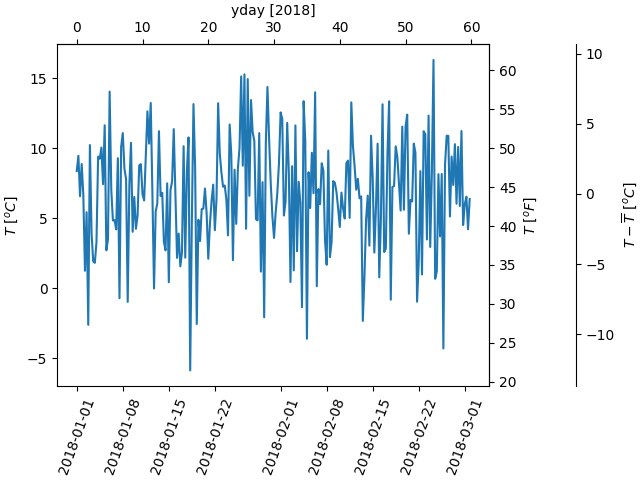
Un último ejemplo traduce np.datetime64 a yearday en el eje x y de Celsius a Fahrenheit en el eje y. Tenga en cuenta la adición de un tercer eje y, y que se puede colocar usando un flotador para el argumento de ubicación

dates = [datetime.datetime(2018, 1, 1) + datetime.timedelta(hours=k * 6)
         for k in range(240)]
temperature = np.random.randn(len(dates)) * 4 + 6.7
fig, ax = plt.subplots(constrained_layout=True)

ax.plot(dates, temperature)
ax.set_ylabel(r'$T\ [^oC]$')
plt.xticks(rotation=70)


def date2yday(x):
    """Convert matplotlib datenum to days since 2018-01-01."""
    y = x - mdates.date2num(datetime.datetime(2018, 1, 1))
    return y


def yday2date(x):
    """Return a matplotlib datenum for *x* days after 2018-01-01."""
    y = x + mdates.date2num(datetime.datetime(2018, 1, 1))
    return y


secax_x = ax.secondary_xaxis('top', functions=(date2yday, yday2date))
secax_x.set_xlabel('yday [2018]')


def celsius_to_fahrenheit(x):
    return x * 1.8 + 32


def fahrenheit_to_celsius(x):
    return (x - 32) / 1.8


secax_y = ax.secondary_yaxis(
    'right', functions=(celsius_to_fahrenheit, fahrenheit_to_celsius))
secax_y.set_ylabel(r'$T\ [^oF]$')


def celsius_to_anomaly(x):
    return (x - np.mean(temperature))


def anomaly_to_celsius(x):
    return (x + np.mean(temperature))


# use of a float for the position:
secax_y2 = ax.secondary_yaxis(
    1.2, functions=(celsius_to_anomaly, anomaly_to_celsius))
secax_y2.set_ylabel(r'$T - \overline{T}\ [^oC]$')


plt.show()

Referencias

En este ejemplo se muestra el uso de las siguientes funciones, métodos, clases y módulos:

• matplotlib.axes.Axes.secondary_xaxis

• matplotlib.axes.Axes.secondary_yaxis