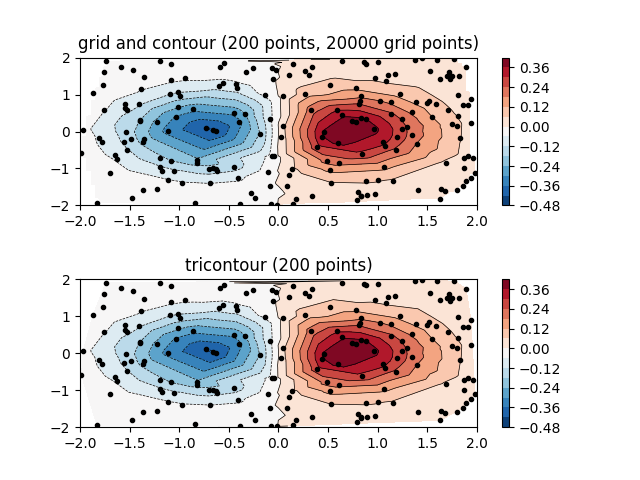
Gráfica de contorno de datos espaciados irregularmente #

Comparación de un gráfico de contorno de datos espaciados irregularmente interpolados en una cuadrícula regular frente a un gráfico de tres contornos para una cuadrícula triangular no estructurada.

Dado que contoury contourfespera que los datos vivan en una cuadrícula regular, trazar un gráfico de contorno de datos espaciados irregularmente requiere métodos diferentes. Las dos opciones son:

Primero interpole los datos a una cuadrícula normal. Esto se puede hacer con medios integrados, por ejemplo, a través de LinearTriInterpolatoro usando una funcionalidad externa, por ejemplo, a través de scipy.interpolate.griddata. Luego grafique los datos interpolados con el habitual contour.
Uso directo tricontouro tricontourfque realizará una triangulación interna.

Este ejemplo muestra ambos métodos en acción.

import matplotlib.pyplot as plt
import matplotlib.tri as tri
import numpy as np

np.random.seed(19680801)
npts = 200
ngridx = 100
ngridy = 200
x = np.random.uniform(-2, 2, npts)
y = np.random.uniform(-2, 2, npts)
z = x * np.exp(-x**2 - y**2)

fig, (ax1, ax2) = plt.subplots(nrows=2)

# -----------------------
# Interpolation on a grid
# -----------------------
# A contour plot of irregularly spaced data coordinates
# via interpolation on a grid.

# Create grid values first.
xi = np.linspace(-2.1, 2.1, ngridx)
yi = np.linspace(-2.1, 2.1, ngridy)

# Linearly interpolate the data (x, y) on a grid defined by (xi, yi).
triang = tri.Triangulation(x, y)
interpolator = tri.LinearTriInterpolator(triang, z)
Xi, Yi = np.meshgrid(xi, yi)
zi = interpolator(Xi, Yi)

# Note that scipy.interpolate provides means to interpolate data on a grid
# as well. The following would be an alternative to the four lines above:
# from scipy.interpolate import griddata
# zi = griddata((x, y), z, (xi[None, :], yi[:, None]), method='linear')

ax1.contour(xi, yi, zi, levels=14, linewidths=0.5, colors='k')
cntr1 = ax1.contourf(xi, yi, zi, levels=14, cmap="RdBu_r")

fig.colorbar(cntr1, ax=ax1)
ax1.plot(x, y, 'ko', ms=3)
ax1.set(xlim=(-2, 2), ylim=(-2, 2))
ax1.set_title('grid and contour (%d points, %d grid points)' %
              (npts, ngridx * ngridy))

# ----------
# Tricontour
# ----------
# Directly supply the unordered, irregularly spaced coordinates
# to tricontour.

ax2.tricontour(x, y, z, levels=14, linewidths=0.5, colors='k')
cntr2 = ax2.tricontourf(x, y, z, levels=14, cmap="RdBu_r")

fig.colorbar(cntr2, ax=ax2)
ax2.plot(x, y, 'ko', ms=3)
ax2.set(xlim=(-2, 2), ylim=(-2, 2))
ax2.set_title('tricontour (%d points)' % npts)

plt.subplots_adjust(hspace=0.5)
plt.show()

cuadrícula y contorno (200 puntos, 20000 puntos de cuadrícula), tricontorno (200 puntos)

Referencias

En este ejemplo se muestra el uso de las siguientes funciones, métodos, clases y módulos:

Galería generada por Sphinx-Gallery