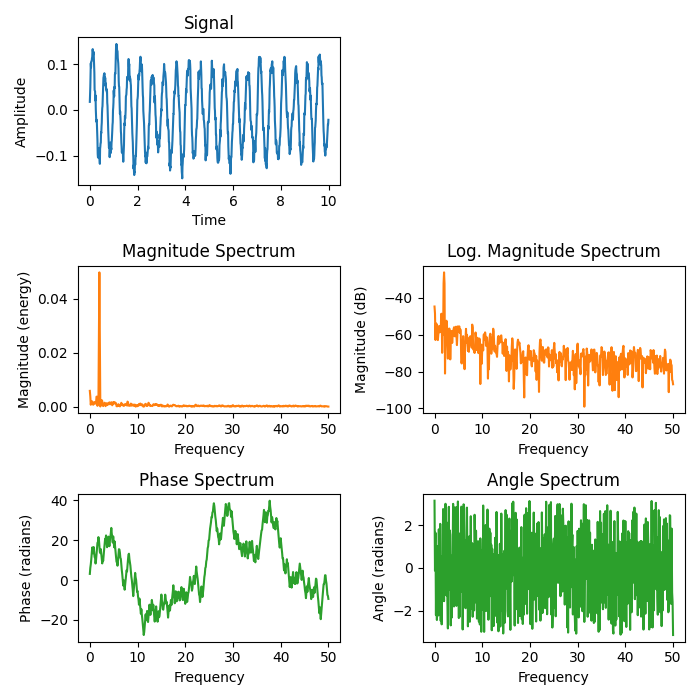
Representaciones de espectro

Los gráficos muestran diferentes representaciones de espectro de una señal sinusoidal con ruido aditivo. Un espectro (frecuencia) de una señal de tiempo discreto se calcula utilizando la transformada rápida de Fourier (FFT).

import matplotlib.pyplot as plt
import numpy as np


np.random.seed(0)

dt = 0.01  # sampling interval
Fs = 1 / dt  # sampling frequency
t = np.arange(0, 10, dt)

# generate noise:
nse = np.random.randn(len(t))
r = np.exp(-t / 0.05)
cnse = np.convolve(nse, r) * dt
cnse = cnse[:len(t)]

s = 0.1 * np.sin(4 * np.pi * t) + cnse  # the signal

fig, axs = plt.subplots(nrows=3, ncols=2, figsize=(7, 7))

# plot time signal:
axs[0, 0].set_title("Signal")
axs[0, 0].plot(t, s, color='C0')
axs[0, 0].set_xlabel("Time")
axs[0, 0].set_ylabel("Amplitude")

# plot different spectrum types:
axs[1, 0].set_title("Magnitude Spectrum")
axs[1, 0].magnitude_spectrum(s, Fs=Fs, color='C1')

axs[1, 1].set_title("Log. Magnitude Spectrum")
axs[1, 1].magnitude_spectrum(s, Fs=Fs, scale='dB', color='C1')

axs[2, 0].set_title("Phase Spectrum ")
axs[2, 0].phase_spectrum(s, Fs=Fs, color='C2')

axs[2, 1].set_title("Angle Spectrum")
axs[2, 1].angle_spectrum(s, Fs=Fs, color='C2')

axs[0, 1].remove()  # don't display empty ax

fig.tight_layout()
plt.show()