Nota
Haga clic aquí para descargar el código de ejemplo completo
Diagrama de dispersión en el eje polar #
El tamaño aumenta radialmente en este ejemplo y el color aumenta con el ángulo (solo para verificar que los símbolos se dispersen correctamente).
import numpy as np
import matplotlib.pyplot as plt
# Fixing random state for reproducibility
np.random.seed(19680801)
# Compute areas and colors
N = 150
r = 2 * np.random.rand(N)
theta = 2 * np.pi * np.random.rand(N)
area = 200 * r**2
colors = theta
fig = plt.figure()
ax = fig.add_subplot(projection='polar')
c = ax.scatter(theta, r, c=colors, s=area, cmap='hsv', alpha=0.75)
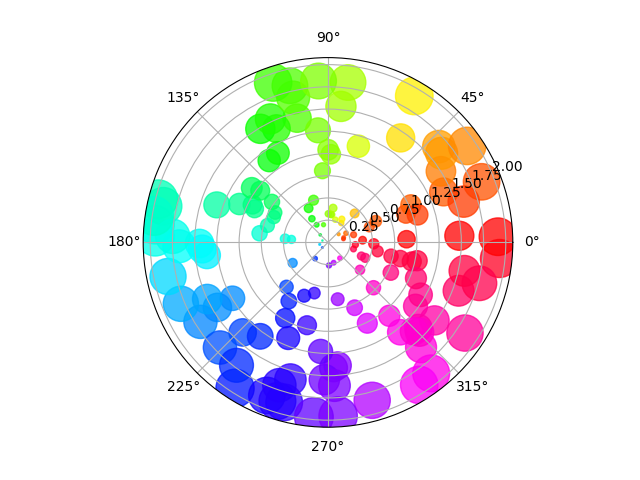
Gráfico de dispersión en el eje polar, con origen desplazado #
La principal diferencia con el gráfico anterior es la configuración del radio de origen, produciendo un anillo. Además, la ubicación del cero theta se establece para rotar la gráfica.
fig = plt.figure()
ax = fig.add_subplot(projection='polar')
c = ax.scatter(theta, r, c=colors, s=area, cmap='hsv', alpha=0.75)
ax.set_rorigin(-2.5)
ax.set_theta_zero_location('W', offset=10)
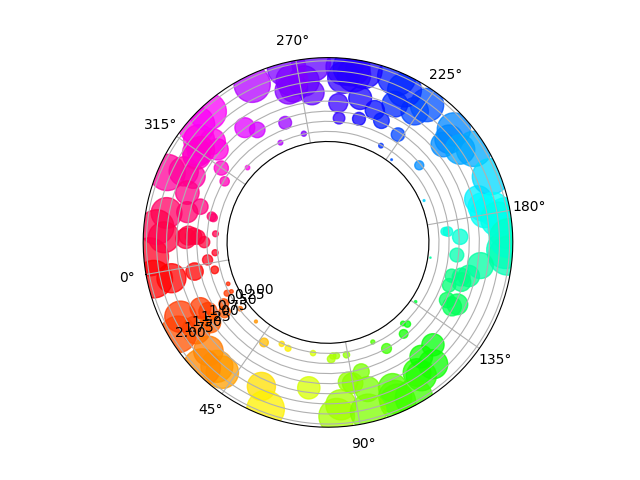
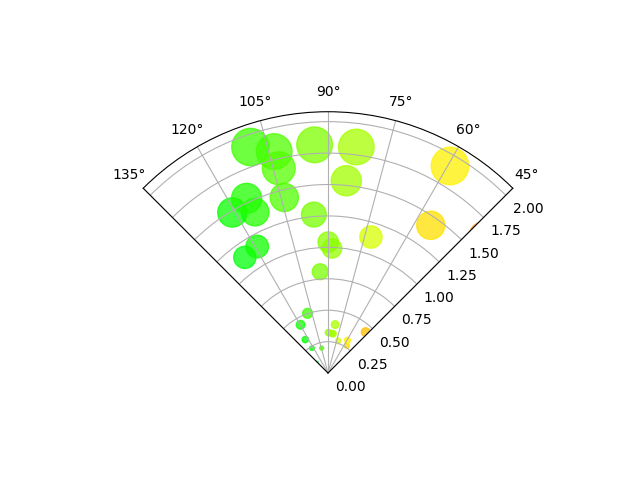
Diagrama de dispersión en el eje polar confinado a un sector #
La principal diferencia con los gráficos anteriores es la configuración de los límites inicial y final de theta, produciendo un sector en lugar de un círculo completo.
fig = plt.figure()
ax = fig.add_subplot(projection='polar')
c = ax.scatter(theta, r, c=colors, s=area, cmap='hsv', alpha=0.75)
ax.set_thetamin(45)
ax.set_thetamax(135)
plt.show()
Referencias
En este ejemplo se muestra el uso de las siguientes funciones, métodos, clases y módulos:
Tiempo total de ejecución del script: (0 minutos 1.739 segundos)