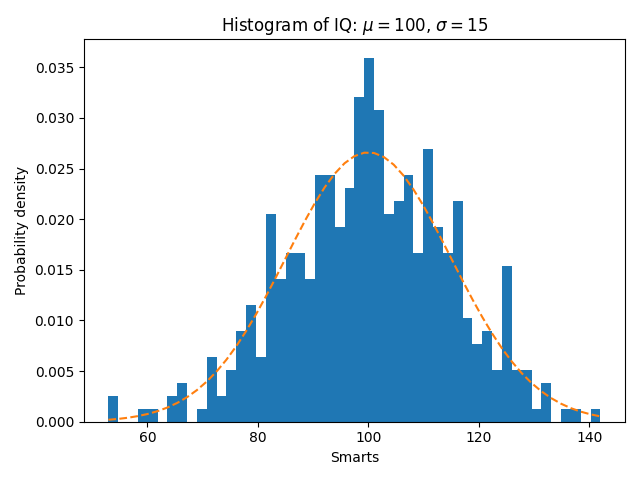
Algunas características de la función de histograma (hist) #

Además del histograma básico, esta demostración muestra algunas características opcionales:

Configuración del número de contenedores de datos.
El parámetro de densidad , que normaliza las alturas de los contenedores para que la integral del histograma sea 1. El histograma resultante es una aproximación de la función de densidad de probabilidad.

La selección de diferentes recuentos y tamaños de contenedores puede afectar significativamente la forma de un histograma. Los documentos de Astropy tienen una gran sección sobre cómo seleccionar estos parámetros.

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(19680801)

# example data
mu = 100  # mean of distribution
sigma = 15  # standard deviation of distribution
x = mu + sigma * np.random.randn(437)

num_bins = 50

fig, ax = plt.subplots()

# the histogram of the data
n, bins, patches = ax.hist(x, num_bins, density=True)

# add a 'best fit' line
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
     np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
ax.plot(bins, y, '--')
ax.set_xlabel('Smarts')
ax.set_ylabel('Probability density')
ax.set_title(r'Histogram of IQ: $\mu=100$, $\sigma=15$')

# Tweak spacing to prevent clipping of ylabel
fig.tight_layout()
plt.show()

$Histograma de CI: $\mu=100$, $\sigma=15$$

Referencias

En este ejemplo se muestra el uso de las siguientes funciones, métodos, clases y módulos:

Galería generada por Sphinx-Gallery