Tipos de proyección de tramas 3D

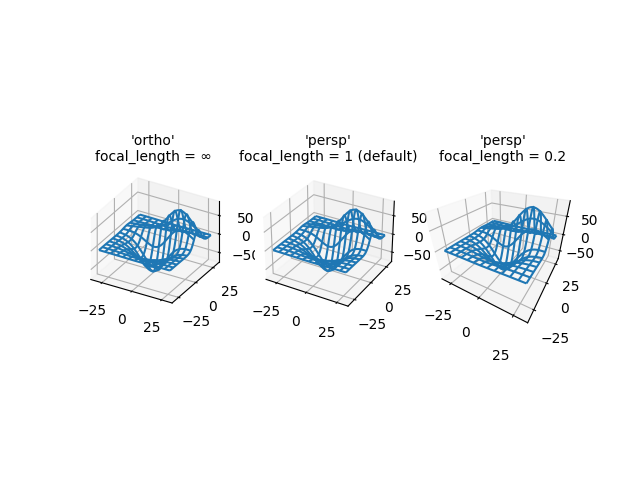
Demuestra las diferentes proyecciones de cámara para gráficos en 3D y los efectos de cambiar la distancia focal para una proyección en perspectiva. Tenga en cuenta que Matplotlib corrige el efecto de 'zoom' al cambiar la distancia focal.

La distancia focal predeterminada de 1 corresponde a un campo de visión (FOV) de 90 grados. Una distancia focal aumentada entre 1 e infinito "aplana" la imagen, mientras que una distancia focal disminuida entre 1 y 0 exagera la perspectiva y le da a la imagen una profundidad más aparente. En el caso límite, una distancia focal de infinito corresponde a una proyección ortográfica después de la corrección del efecto zoom.

Puede calcular la distancia focal de un FOV a través de la ecuación:

\[1 / \tan (\mathrm{FOV} / 2)\]

O viceversa:

\[\mathrm{FOV} = 2 \arctan (1 / \mathrm{focal length})\]

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt


fig, axs = plt.subplots(1, 3, subplot_kw={'projection': '3d'})

# Get the test data
X, Y, Z = axes3d.get_test_data(0.05)

# Plot the data
for ax in axs:
    ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)

# Set the orthographic projection.
axs[0].set_proj_type('ortho')  # FOV = 0 deg
axs[0].set_title("'ortho'\nfocal_length = ∞", fontsize=10)

# Set the perspective projections
axs[1].set_proj_type('persp')  # FOV = 90 deg
axs[1].set_title("'persp'\nfocal_length = 1 (default)", fontsize=10)

axs[2].set_proj_type('persp', focal_length=0.2)  # FOV = 157.4 deg
axs[2].set_title("'persp'\nfocal_length = 0.2", fontsize=10)

plt.show()