Trazar una elipse de confianza de un conjunto de datos bidimensional

Este ejemplo muestra cómo trazar una elipse de confianza de un conjunto de datos bidimensional, utilizando su coeficiente de correlación de Pearson.

El enfoque que se utiliza para obtener la geometría correcta se explica y prueba aquí:

https://carstenschelp.github.io/2018/09/14/Plot_Confidence_Ellipse_001.html

El método evita el uso de un algoritmo iterativo de descomposición propia y hace uso del hecho de que una matriz de covarianza normalizada (compuesta por coeficientes de correlación de Pearson y unos) es particularmente fácil de manejar.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
import matplotlib.transforms as transforms

La propia función de trazado

Esta función representa gráficamente la elipse de confianza de la covarianza de las variables tipo matriz dadas x e y. La elipse se traza en el eje dado de ejes-objeto.

Los radios de la elipse se pueden controlar mediante n_std, que es el número de desviaciones estándar. El valor predeterminado es 3, lo que hace que la elipse encierre el 98,9 % de los puntos si los datos se distribuyen normalmente como en estos ejemplos (3 desviaciones estándar en 1-D contienen el 99,7 % de los datos, que es el 98,9 % de los datos en 2-D). D).

def confidence_ellipse(x, y, ax, n_std=3.0, facecolor='none', **kwargs):
    """
    Create a plot of the covariance confidence ellipse of *x* and *y*.

    Parameters
    ----------
    x, y : array-like, shape (n, )
        Input data.

    ax : matplotlib.axes.Axes
        The axes object to draw the ellipse into.

    n_std : float
        The number of standard deviations to determine the ellipse's radiuses.

    **kwargs
        Forwarded to `~matplotlib.patches.Ellipse`

    Returns
    -------
    matplotlib.patches.Ellipse
    """
    if x.size != y.size:
        raise ValueError("x and y must be the same size")

    cov = np.cov(x, y)
    pearson = cov[0, 1]/np.sqrt(cov[0, 0] * cov[1, 1])
    # Using a special case to obtain the eigenvalues of this
    # two-dimensional dataset.
    ell_radius_x = np.sqrt(1 + pearson)
    ell_radius_y = np.sqrt(1 - pearson)
    ellipse = Ellipse((0, 0), width=ell_radius_x * 2, height=ell_radius_y * 2,
                      facecolor=facecolor, **kwargs)

    # Calculating the standard deviation of x from
    # the squareroot of the variance and multiplying
    # with the given number of standard deviations.
    scale_x = np.sqrt(cov[0, 0]) * n_std
    mean_x = np.mean(x)

    # calculating the standard deviation of y ...
    scale_y = np.sqrt(cov[1, 1]) * n_std
    mean_y = np.mean(y)

    transf = transforms.Affine2D() \
        .rotate_deg(45) \
        .scale(scale_x, scale_y) \
        .translate(mean_x, mean_y)

    ellipse.set_transform(transf + ax.transData)
    return ax.add_patch(ellipse)

Una función auxiliar para crear un conjunto de datos correlacionados

Crea un conjunto de datos bidimensional aleatorio con la media bidimensional (mu) y las dimensiones (escala) especificadas. La correlación se puede controlar mediante el parámetro 'dependencia', una matriz de 2x2.

def get_correlated_dataset(n, dependency, mu, scale):
    latent = np.random.randn(n, 2)
    dependent = latent.dot(dependency)
    scaled = dependent * scale
    scaled_with_offset = scaled + mu
    # return x and y of the new, correlated dataset
    return scaled_with_offset[:, 0], scaled_with_offset[:, 1]

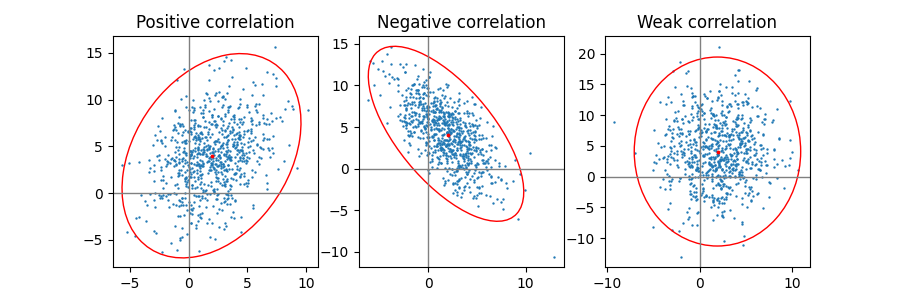
Correlación positiva, negativa y débil

Tenga en cuenta que la forma de la correlación débil (derecha) es una elipse, no un círculo porque x e y tienen escalas diferentes. Sin embargo, el hecho de que x e y no están correlacionados se muestra porque los ejes de la elipse están alineados con los ejes x e y del sistema de coordenadas.

np.random.seed(0)

PARAMETERS = {
    'Positive correlation': [[0.85, 0.35],
                             [0.15, -0.65]],
    'Negative correlation': [[0.9, -0.4],
                             [0.1, -0.6]],
    'Weak correlation': [[1, 0],
                         [0, 1]],
}

mu = 2, 4
scale = 3, 5

fig, axs = plt.subplots(1, 3, figsize=(9, 3))
for ax, (title, dependency) in zip(axs, PARAMETERS.items()):
    x, y = get_correlated_dataset(800, dependency, mu, scale)
    ax.scatter(x, y, s=0.5)

    ax.axvline(c='grey', lw=1)
    ax.axhline(c='grey', lw=1)

    confidence_ellipse(x, y, ax, edgecolor='red')

    ax.scatter(mu[0], mu[1], c='red', s=3)
    ax.set_title(title)

plt.show()

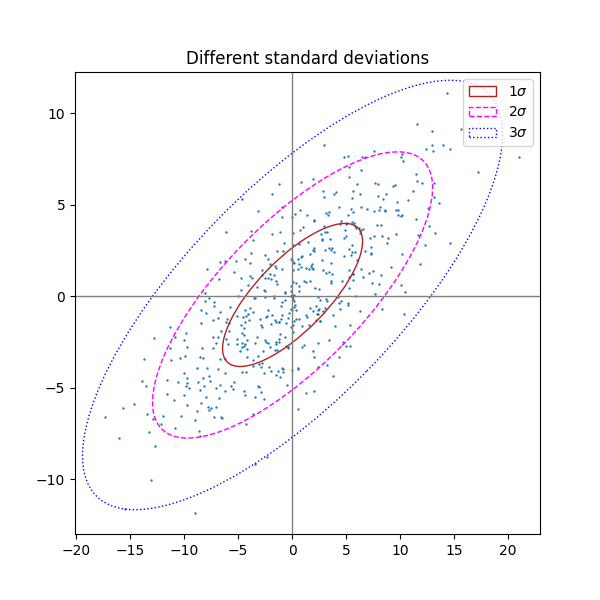
Número diferente de desviaciones estándar

Un gráfico con n_std = 3 (azul), 2 (púrpura) y 1 (rojo)

fig, ax_nstd = plt.subplots(figsize=(6, 6))

dependency_nstd = [[0.8, 0.75],
                   [-0.2, 0.35]]
mu = 0, 0
scale = 8, 5

ax_nstd.axvline(c='grey', lw=1)
ax_nstd.axhline(c='grey', lw=1)

x, y = get_correlated_dataset(500, dependency_nstd, mu, scale)
ax_nstd.scatter(x, y, s=0.5)

confidence_ellipse(x, y, ax_nstd, n_std=1,
                   label=r'$1\sigma$', edgecolor='firebrick')
confidence_ellipse(x, y, ax_nstd, n_std=2,
                   label=r'$2\sigma$', edgecolor='fuchsia', linestyle='--')
confidence_ellipse(x, y, ax_nstd, n_std=3,
                   label=r'$3\sigma$', edgecolor='blue', linestyle=':')

ax_nstd.scatter(mu[0], mu[1], c='red', s=3)
ax_nstd.set_title('Different standard deviations')
ax_nstd.legend()
plt.show()

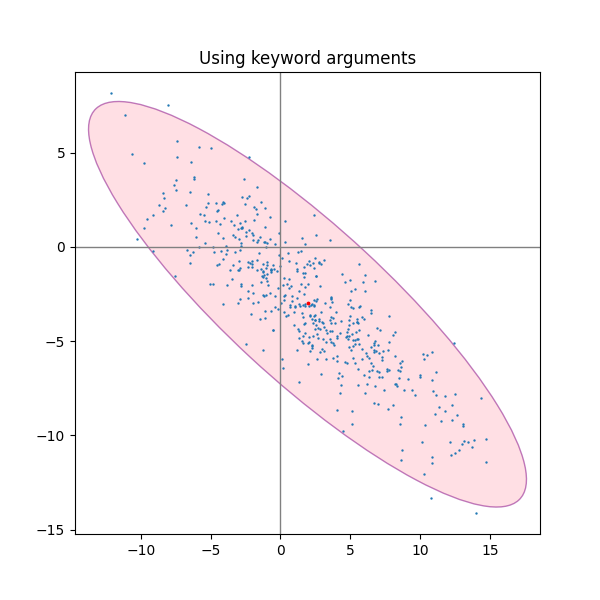
Usando los argumentos de palabras clave

Utilice los argumentos de palabra clave especificados para matplotlib.patches.Patchque la elipse se represente de diferentes maneras.

fig, ax_kwargs = plt.subplots(figsize=(6, 6))
dependency_kwargs = [[-0.8, 0.5],
                     [-0.2, 0.5]]
mu = 2, -3
scale = 6, 5

ax_kwargs.axvline(c='grey', lw=1)
ax_kwargs.axhline(c='grey', lw=1)

x, y = get_correlated_dataset(500, dependency_kwargs, mu, scale)
# Plot the ellipse with zorder=0 in order to demonstrate
# its transparency (caused by the use of alpha).
confidence_ellipse(x, y, ax_kwargs,
                   alpha=0.5, facecolor='pink', edgecolor='purple', zorder=0)

ax_kwargs.scatter(x, y, s=0.5)
ax_kwargs.scatter(mu[0], mu[1], c='red', s=3)
ax_kwargs.set_title('Using keyword arguments')

fig.subplots_adjust(hspace=0.25)
plt.show()

Referencias

En este ejemplo se muestra el uso de las siguientes funciones, métodos, clases y módulos:

• matplotlib.transforms.Affine2D

• matplotlib.patches.Ellipse