Serie de tiempo Histograma

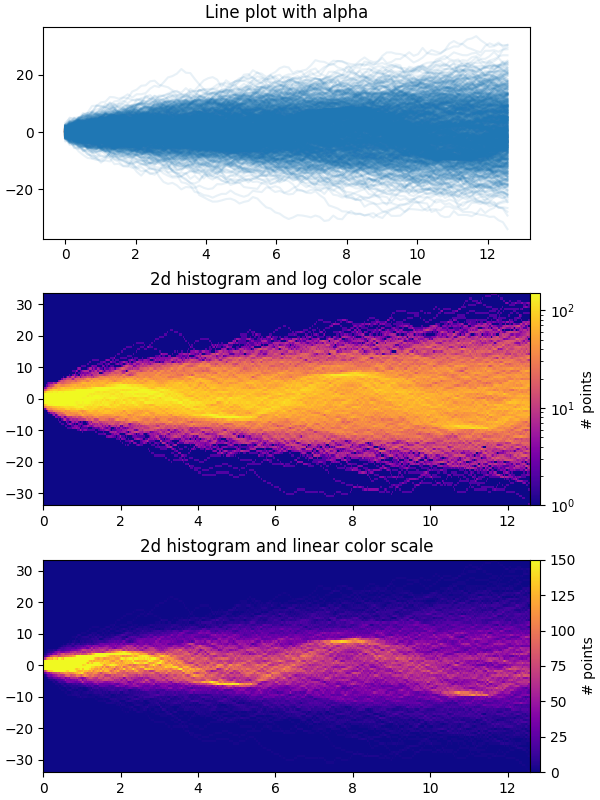
Este ejemplo demuestra cómo visualizar eficientemente grandes cantidades de series de tiempo de una manera que podría revelar subestructuras y patrones ocultos que no son inmediatamente obvios, y mostrarlos de una manera visualmente atractiva.

En este ejemplo, generamos múltiples series de "señales" sinusoidales que están enterradas bajo un mayor número de series de "ruido/fondo" de recorrido aleatorio. Para una caminata aleatoria gaussiana no sesgada con una desviación estándar de σ, la desviación RMS del origen después de n pasos es σ*sqrt(n). Entonces, para mantener las sinusoides visibles en la misma escala que los paseos aleatorios, escalamos la amplitud por el RMS del paseo aleatorio. Además, también introducimos un pequeño desplazamiento aleatorio phi para cambiar los senos hacia la izquierda/derecha, y algo de ruido aleatorio aditivo para cambiar los puntos de datos individuales hacia arriba/abajo para hacer que la señal sea un poco más "realista" (no esperaría un seno perfecto). wave para que aparezca en sus datos).

El primer gráfico muestra la forma típica de visualizar varias series de tiempo superponiéndolas una encima de otra con plt.plotun valor pequeño de alpha. Los gráficos segundo y tercero muestran cómo reinterpretar los datos como un histograma 2d, con interpolación opcional entre puntos de datos, usando np.histogram2dy plt.pcolormesh.

from copy import copy
import time

import numpy as np
import numpy.matlib
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm

fig, axes = plt.subplots(nrows=3, figsize=(6, 8), constrained_layout=True)

# Make some data; a 1D random walk + small fraction of sine waves
num_series = 1000
num_points = 100
SNR = 0.10  # Signal to Noise Ratio
x = np.linspace(0, 4 * np.pi, num_points)
# Generate unbiased Gaussian random walks
Y = np.cumsum(np.random.randn(num_series, num_points), axis=-1)
# Generate sinusoidal signals
num_signal = int(round(SNR * num_series))
phi = (np.pi / 8) * np.random.randn(num_signal, 1)  # small random offset
Y[-num_signal:] = (
    np.sqrt(np.arange(num_points))[None, :]  # random walk RMS scaling factor
    * (np.sin(x[None, :] - phi)
       + 0.05 * np.random.randn(num_signal, num_points))  # small random noise
)


# Plot series using `plot` and a small value of `alpha`. With this view it is
# very difficult to observe the sinusoidal behavior because of how many
# overlapping series there are. It also takes a bit of time to run because so
# many individual artists need to be generated.
tic = time.time()
axes[0].plot(x, Y.T, color="C0", alpha=0.1)
toc = time.time()
axes[0].set_title("Line plot with alpha")
print(f"{toc-tic:.3f} sec. elapsed")


# Now we will convert the multiple time series into a histogram. Not only will
# the hidden signal be more visible, but it is also a much quicker procedure.
tic = time.time()
# Linearly interpolate between the points in each time series
num_fine = 800
x_fine = np.linspace(x.min(), x.max(), num_fine)
y_fine = np.empty((num_series, num_fine), dtype=float)
for i in range(num_series):
    y_fine[i, :] = np.interp(x_fine, x, Y[i, :])
y_fine = y_fine.flatten()
x_fine = np.matlib.repmat(x_fine, num_series, 1).flatten()


# Plot (x, y) points in 2d histogram with log colorscale
# It is pretty evident that there is some kind of structure under the noise
# You can tune vmax to make signal more visible
cmap = copy(plt.cm.plasma)
cmap.set_bad(cmap(0))
h, xedges, yedges = np.histogram2d(x_fine, y_fine, bins=[400, 100])
pcm = axes[1].pcolormesh(xedges, yedges, h.T, cmap=cmap,
                         norm=LogNorm(vmax=1.5e2), rasterized=True)
fig.colorbar(pcm, ax=axes[1], label="# points", pad=0)
axes[1].set_title("2d histogram and log color scale")

# Same data but on linear color scale
pcm = axes[2].pcolormesh(xedges, yedges, h.T, cmap=cmap,
                         vmax=1.5e2, rasterized=True)
fig.colorbar(pcm, ax=axes[2], label="# points", pad=0)
axes[2].set_title("2d histogram and linear color scale")

toc = time.time()
print(f"{toc-tic:.3f} sec. elapsed")
plt.show()

0.219 sec. elapsed
0.071 sec. elapsed

Referencias

En este ejemplo se muestra el uso de las siguientes funciones, métodos, clases y módulos:

• matplotlib.axes.Axes.pcolormesh/matplotlib.pyplot.pcolormesh

• matplotlib.figure.Figure.colorbar