Contorno del espacio de solución de optimizaciones

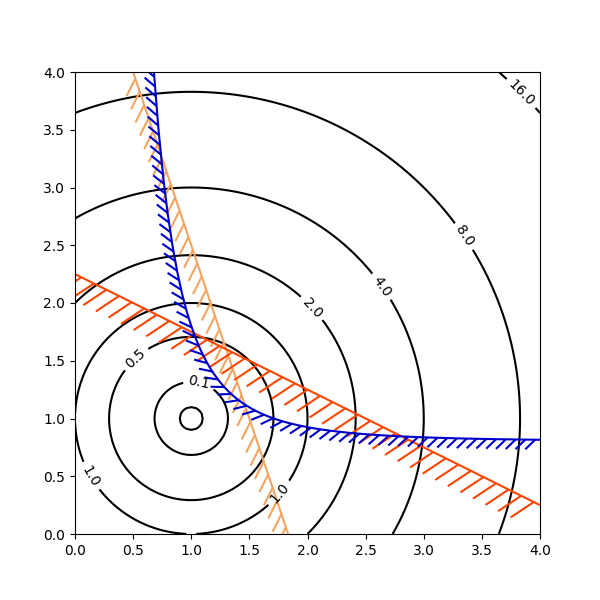
El trazado de contornos es particularmente útil cuando se ilustra el espacio de solución de problemas de optimización. No solo se axes.Axes.contourpuede utilizar para representar la topografía de la función objetivo, sino que también se puede utilizar para generar curvas de contorno de las funciones de restricción. Las líneas de restricción se pueden dibujar TickedStrokepara distinguir los lados válidos e inválidos de los límites de restricción.

axes.Axes.contourgenera curvas con valores mayores a la izquierda del contorno. El parámetro de ángulo se mide cero adelante con valores crecientes a la izquierda. En consecuencia, cuando se utiliza TickedStrokepara ilustrar una restricción en un problema de optimización típico, el ángulo debe establecerse entre cero y 180 grados.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import patheffects

fig, ax = plt.subplots(figsize=(6, 6))

nx = 101
ny = 105

# Set up survey vectors
xvec = np.linspace(0.001, 4.0, nx)
yvec = np.linspace(0.001, 4.0, ny)

# Set up survey matrices.  Design disk loading and gear ratio.
x1, x2 = np.meshgrid(xvec, yvec)

# Evaluate some stuff to plot
obj = x1**2 + x2**2 - 2*x1 - 2*x2 + 2
g1 = -(3*x1 + x2 - 5.5)
g2 = -(x1 + 2*x2 - 4.5)
g3 = 0.8 + x1**-3 - x2

cntr = ax.contour(x1, x2, obj, [0.01, 0.1, 0.5, 1, 2, 4, 8, 16],
                  colors='black')
ax.clabel(cntr, fmt="%2.1f", use_clabeltext=True)

cg1 = ax.contour(x1, x2, g1, [0], colors='sandybrown')
plt.setp(cg1.collections,
         path_effects=[patheffects.withTickedStroke(angle=135)])

cg2 = ax.contour(x1, x2, g2, [0], colors='orangered')
plt.setp(cg2.collections,
         path_effects=[patheffects.withTickedStroke(angle=60, length=2)])

cg3 = ax.contour(x1, x2, g3, [0], colors='mediumblue')
plt.setp(cg3.collections,
         path_effects=[patheffects.withTickedStroke(spacing=7)])

ax.set_xlim(0, 4)
ax.set_ylim(0, 4)

plt.show()