Rellenar entre y alfa

La fill_betweenfunción genera una región sombreada entre un límite mínimo y máximo que es útil para ilustrar rangos. Tiene un whereargumento muy útil para combinar el llenado con rangos lógicos, por ejemplo, para simplemente completar una curva sobre algún valor de umbral.

En su nivel más básico, fill_betweense puede utilizar para mejorar la apariencia visual de un gráfico. Comparemos dos gráficos de datos financieros con un diagrama de línea simple a la izquierda y una línea llena a la derecha.

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.cbook as cbook


# load up some sample financial data
r = (cbook.get_sample_data('goog.npz', np_load=True)['price_data']
     .view(np.recarray))
# create two subplots with the shared x and y axes
fig, (ax1, ax2) = plt.subplots(1, 2, sharex=True, sharey=True)

pricemin = r.close.min()

ax1.plot(r.date, r.close, lw=2)
ax2.fill_between(r.date, pricemin, r.close, alpha=0.7)

for ax in ax1, ax2:
    ax.grid(True)
    ax.label_outer()

ax1.set_ylabel('price')

fig.suptitle('Google (GOOG) daily closing price')
fig.autofmt_xdate()

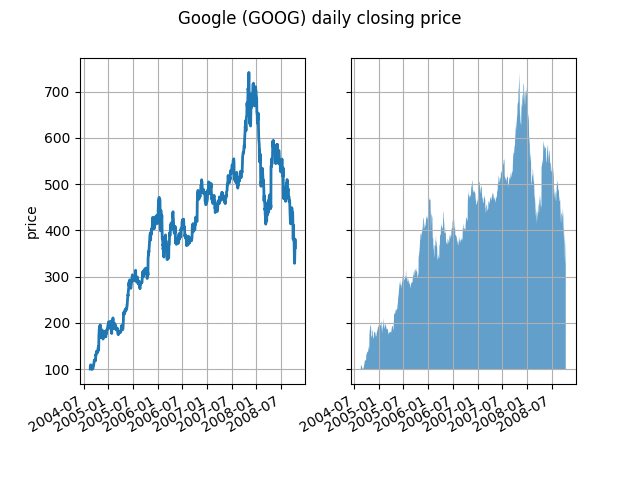
El canal alfa no es necesario aquí, pero se puede usar para suavizar los colores para obtener tramas más atractivas visualmente. En otros ejemplos, como veremos a continuación, el canal alfa es funcionalmente útil ya que las regiones sombreadas pueden superponerse y alfa le permite ver ambas. Tenga en cuenta que el formato postscript no es compatible con alfa (esta es una limitación de postscript, no una limitación de matplotlib), por lo que cuando use alfa guarde sus figuras en PNG, PDF o SVG.

Nuestro siguiente ejemplo calcula dos poblaciones de caminantes aleatorios con una media y una desviación estándar diferentes de las distribuciones normales a partir de las cuales se extraen los pasos. Usamos regiones rellenas para trazar +/- una desviación estándar de la posición media de la población. Aquí el canal alfa es útil, no solo estético.

# Fixing random state for reproducibility
np.random.seed(19680801)

Nsteps, Nwalkers = 100, 250
t = np.arange(Nsteps)

# an (Nsteps x Nwalkers) array of random walk steps
S1 = 0.004 + 0.02*np.random.randn(Nsteps, Nwalkers)
S2 = 0.002 + 0.01*np.random.randn(Nsteps, Nwalkers)

# an (Nsteps x Nwalkers) array of random walker positions
X1 = S1.cumsum(axis=0)
X2 = S2.cumsum(axis=0)


# Nsteps length arrays empirical means and standard deviations of both
# populations over time
mu1 = X1.mean(axis=1)
sigma1 = X1.std(axis=1)
mu2 = X2.mean(axis=1)
sigma2 = X2.std(axis=1)

# plot it!
fig, ax = plt.subplots(1)
ax.plot(t, mu1, lw=2, label='mean population 1')
ax.plot(t, mu2, lw=2, label='mean population 2')
ax.fill_between(t, mu1+sigma1, mu1-sigma1, facecolor='C0', alpha=0.4)
ax.fill_between(t, mu2+sigma2, mu2-sigma2, facecolor='C1', alpha=0.4)
ax.set_title(r'random walkers empirical $\mu$ and $\pm \sigma$ interval')
ax.legend(loc='upper left')
ax.set_xlabel('num steps')
ax.set_ylabel('position')
ax.grid()

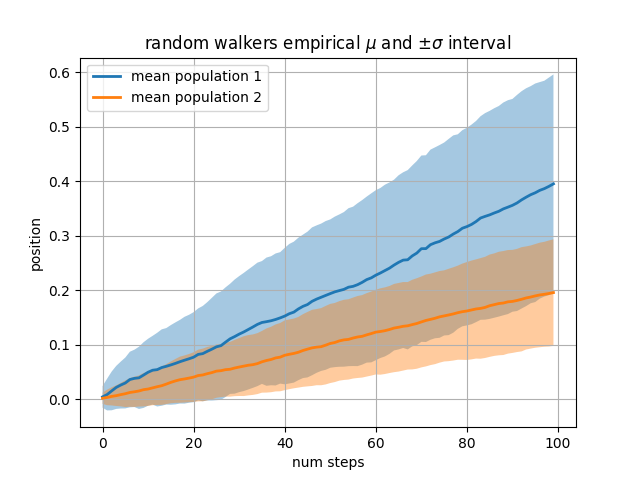
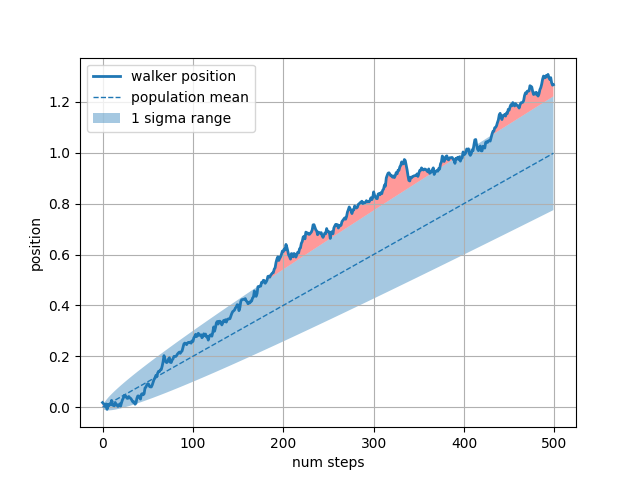
El whereargumento de palabra clave es muy útil para resaltar ciertas regiones del gráfico. wheretoma una máscara booleana de la misma longitud que los argumentos x, ymin e ymax, y solo completa la región donde la máscara booleana es verdadera. En el siguiente ejemplo, simulamos un solo caminante aleatorio y calculamos la media analítica y la desviación estándar de las posiciones de la población. La media de la población se muestra como la línea discontinua, y la desviación de más/menos un sigma de la media se muestra como la región rellena. Usamos la máscara where para encontrar la región donde el caminante está fuera del límite de sigma y sombreamos esa región en rojo.X > upper_bound

# Fixing random state for reproducibility
np.random.seed(1)

Nsteps = 500
t = np.arange(Nsteps)

mu = 0.002
sigma = 0.01

# the steps and position
S = mu + sigma*np.random.randn(Nsteps)
X = S.cumsum()

# the 1 sigma upper and lower analytic population bounds
lower_bound = mu*t - sigma*np.sqrt(t)
upper_bound = mu*t + sigma*np.sqrt(t)

fig, ax = plt.subplots(1)
ax.plot(t, X, lw=2, label='walker position')
ax.plot(t, mu*t, lw=1, label='population mean', color='C0', ls='--')
ax.fill_between(t, lower_bound, upper_bound, facecolor='C0', alpha=0.4,
                label='1 sigma range')
ax.legend(loc='upper left')

# here we use the where argument to only fill the region where the
# walker is above the population 1 sigma boundary
ax.fill_between(t, upper_bound, X, where=X > upper_bound, fc='red', alpha=0.4)
ax.fill_between(t, lower_bound, X, where=X < lower_bound, fc='red', alpha=0.4)
ax.set_xlabel('num steps')
ax.set_ylabel('position')
ax.grid()

Otro uso útil de las regiones rellenas es resaltar los tramos horizontales o verticales de un eje; para eso, Matplotlib tiene las funciones auxiliares axhspany axvspan. Vea la demostración de axhspan .

plt.show()