de demostración de Asinh

Ilustración de la asinhescala del eje, que utiliza la transformación

\[a \rightarrow a_0 \sinh^{-1} (a / a_0)\]

Para valores de coordenadas cercanos a cero (es decir, mucho más pequeños que el "ancho lineal"\(a_0\)), esto deja los valores esencialmente sin cambios:

\[a \rightarrow a + \mathcal{O}(a^3)\]

pero para valores mayores (es decir\(|a| \gg a_0\), esto es asintóticamente

\[a \rightarrow a_0 \, \mathrm{sgn}(a) \ln |a| + \mathcal{O}(1)\]

Al igual que con la symlogescala, esto permite trazar cantidades que cubren un rango dinámico muy amplio que incluye valores tanto positivos como negativos. Sin embargo, symlogimplica una transformación que tiene discontinuidades en su gradiente porque se construye a partir de transformaciones lineales y logarítmicas separadas . La asinhescala utiliza una transformación que es suave para todos los valores (finitos), que es matemáticamente más clara y reduce los artefactos visuales asociados con una transición abrupta entre regiones lineales y logarítmicas de la gráfica.

Nota

scale.AsinhScalees experimental y la API puede cambiar.

Ver AsinhScale, SymmetricalLogScale.

import numpy as np
import matplotlib.pyplot as plt

# Prepare sample values for variations on y=x graph:
x = np.linspace(-3, 6, 500)

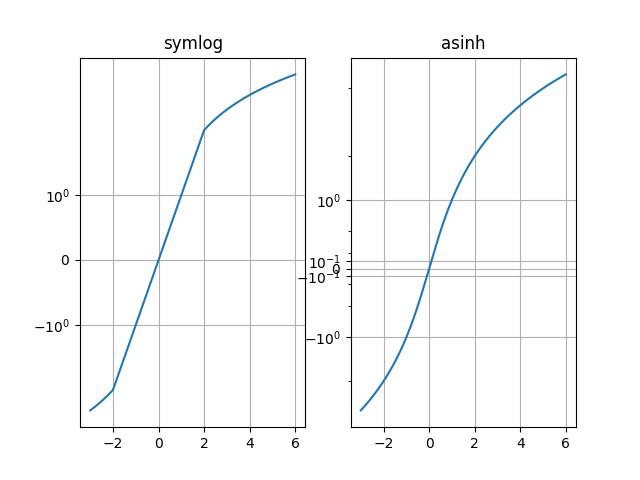
Compare el comportamiento de "symlog" y "asinh" en el gráfico de muestra y=x, donde hay un gradiente discontinuo en "symlog" cerca de y=2:

fig1 = plt.figure()
ax0, ax1 = fig1.subplots(1, 2, sharex=True)

ax0.plot(x, x)
ax0.set_yscale('symlog')
ax0.grid()
ax0.set_title('symlog')

ax1.plot(x, x)
ax1.set_yscale('asinh')
ax1.grid()
ax1.set_title('asinh')

Text(0.5, 1.0, 'asinh')

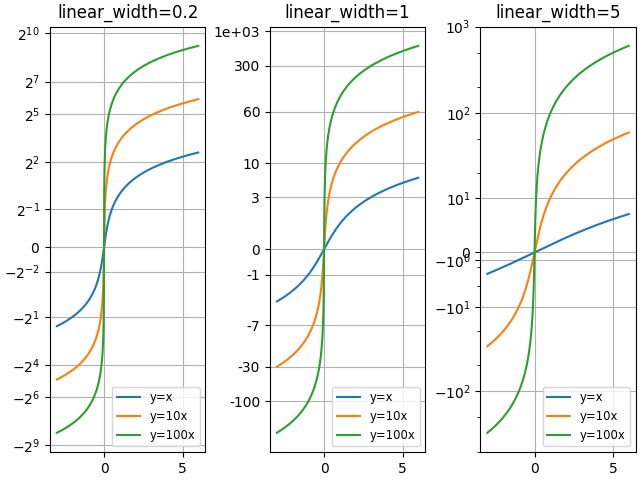
Compare gráficos "asinh" con diferentes parámetros de escala "linear_width":

fig2 = plt.figure(constrained_layout=True)
axs = fig2.subplots(1, 3, sharex=True)
for ax, (a0, base) in zip(axs, ((0.2, 2), (1.0, 0), (5.0, 10))):
    ax.set_title('linear_width={:.3g}'.format(a0))
    ax.plot(x, x, label='y=x')
    ax.plot(x, 10*x, label='y=10x')
    ax.plot(x, 100*x, label='y=100x')
    ax.set_yscale('asinh', linear_width=a0, base=base)
    ax.grid()
    ax.legend(loc='best', fontsize='small')

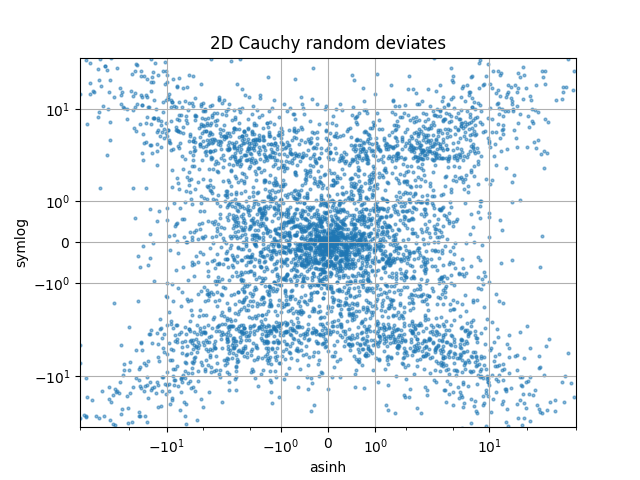
Compare las escalas "symlog" y "asinh" en números aleatorios 2D distribuidos por Cauchy, donde uno puede ver artefactos más sutiles cerca de y = 2 debido a la discontinuidad del gradiente en "symlog":

fig3 = plt.figure()
ax = fig3.subplots(1, 1)
r = 3 * np.tan(np.random.uniform(-np.pi / 2.02, np.pi / 2.02,
                                 size=(5000,)))
th = np.random.uniform(0, 2*np.pi, size=r.shape)

ax.scatter(r * np.cos(th), r * np.sin(th), s=4, alpha=0.5)
ax.set_xscale('asinh')
ax.set_yscale('symlog')
ax.set_xlabel('asinh')
ax.set_ylabel('symlog')
ax.set_title('2D Cauchy random deviates')
ax.set_xlim(-50, 50)
ax.set_ylim(-50, 50)
ax.grid()

plt.show()

Referencias

• matplotlib.scale.AsinhScale

• matplotlib.ticker.AsinhLocator

• matplotlib.scale.SymmetricalLogScale