Normalización del mapa de colores

Los objetos que usan mapas de colores por defecto asignan linealmente los colores en el mapa de colores desde los valores de datos vmin hasta vmax . Por ejemplo:

pcm = ax.pcolormesh(x, y, Z, vmin=-1., vmax=1., cmap='RdBu_r')

mapeará los datos en Z linealmente de -1 a +1, por lo que Z=0 dará un color en el centro del mapa de colores RdBu_r (blanco en este caso).

Matplotlib hace este mapeo en dos pasos, con una normalización de los datos de entrada a [0, 1] que ocurre primero y luego se mapea en los índices en el mapa de colores. Las normalizaciones son clases definidas en el matplotlib.colors()módulo. La normalización lineal predeterminada es matplotlib.colors.Normalize().

Los artistas que asignan datos a color pasan los argumentos vmin y vmax para construir una matplotlib.colors.Normalize()instancia y luego la llaman:

In [1]: import matplotlib as mpl

In [2]: norm = mpl.colors.Normalize(vmin=-1, vmax=1)

In [3]: norm(0)
Out[3]: 0.5

Sin embargo, a veces hay casos en los que es útil asignar datos a mapas de color de forma no lineal.

logarítmico

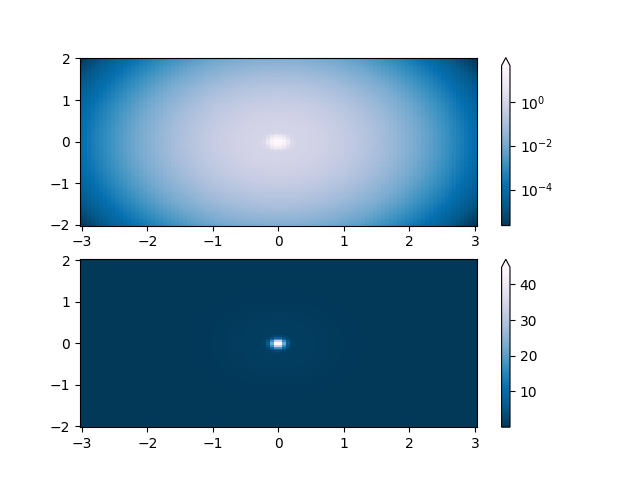
Una de las transformaciones más comunes es graficar datos tomando su logaritmo (en base 10). Esta transformación es útil para mostrar cambios en escalas dispares. El uso colors.LogNormnormaliza los datos a través de \(log_{10}\). En el siguiente ejemplo, hay dos protuberancias, una mucho más pequeña que la otra. Usando colors.LogNorm, la forma y la ubicación de cada protuberancia se pueden ver claramente:

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import matplotlib.cbook as cbook
from matplotlib import cm

N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]

# A low hump with a spike coming out of the top right.  Needs to have
# z/colour axis on a log scale so we see both hump and spike.  linear
# scale only shows the spike.
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X * 10)**2 - (Y * 10)**2)
Z = Z1 + 50 * Z2

fig, ax = plt.subplots(2, 1)

pcm = ax[0].pcolor(X, Y, Z,
                   norm=colors.LogNorm(vmin=Z.min(), vmax=Z.max()),
                   cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='max')

pcm = ax[1].pcolor(X, Y, Z, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='max')
plt.show()

Centrado

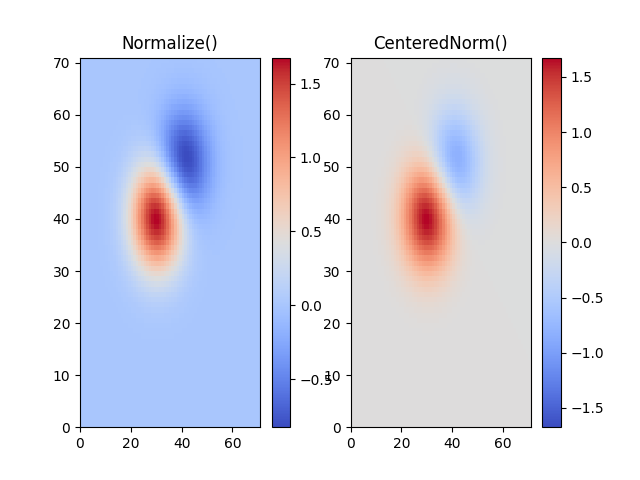
En muchos casos, los datos son simétricos alrededor de un centro, por ejemplo, anomalías positivas y negativas alrededor de un centro 0. En este caso, nos gustaría que el centro se mapee en 0.5 y que se mapee el punto de datos con la mayor desviación del centro. a 1,0, si su valor es mayor que el centro, o 0,0 en caso contrario. La norma colors.CenteredNormcrea tal mapeo automáticamente. Es muy adecuado para combinarlo con un mapa de colores divergente que utiliza bordes de diferentes colores que se encuentran en el centro en un color no saturado.

Si el centro de simetría es diferente de 0, se puede establecer con el argumento vcenter . Para la escala logarítmica en ambos lados del centro, consulte a colors.SymLogNormcontinuación; para aplicar una asignación diferente por encima y por debajo del centro, utilice a colors.TwoSlopeNormcontinuación.

delta = 0.1
x = np.arange(-3.0, 4.001, delta)
y = np.arange(-4.0, 3.001, delta)
X, Y = np.meshgrid(x, y)
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (0.9*Z1 - 0.5*Z2) * 2

# select a divergent colormap
cmap = cm.coolwarm

fig, (ax1, ax2) = plt.subplots(ncols=2)
pc = ax1.pcolormesh(Z, cmap=cmap)
fig.colorbar(pc, ax=ax1)
ax1.set_title('Normalize()')

pc = ax2.pcolormesh(Z, norm=colors.CenteredNorm(), cmap=cmap)
fig.colorbar(pc, ax=ax2)
ax2.set_title('CenteredNorm()')

plt.show()

Logarítmico simétrico

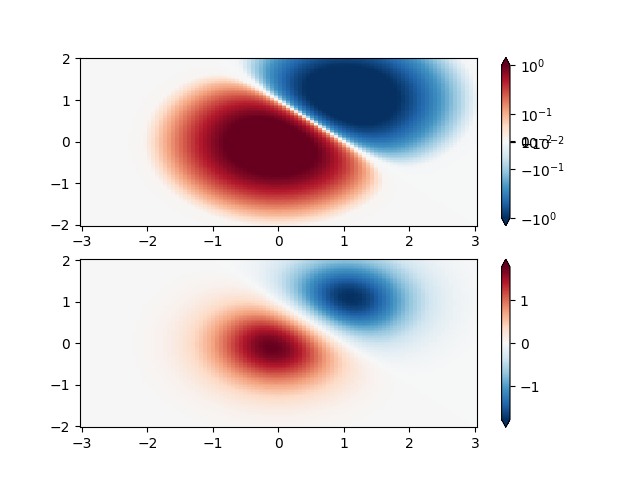
Del mismo modo, a veces sucede que hay datos que son positivos y negativos, pero aún nos gustaría aplicar una escala logarítmica a ambos. En este caso, los números negativos también se escalan logarítmicamente y se asignan a números más pequeños; por ejemplo, si vmin=-vmax, entonces los números negativos se asignan de 0 a 0,5 y los positivos de 0,5 a 1.

Dado que el logaritmo de los valores cercanos a cero tiende hacia el infinito, es necesario mapear linealmente un pequeño rango alrededor de cero. El parámetro linthresh permite al usuario especificar el tamaño de este rango ( -linthresh , linthresh ). El tamaño de este rango en el mapa de colores lo establece linscale . Cuando linscale == 1.0 (el valor predeterminado), el espacio utilizado para las mitades positiva y negativa del rango lineal será igual a una década en el rango logarítmico.

N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (Z1 - Z2) * 2

fig, ax = plt.subplots(2, 1)

pcm = ax[0].pcolormesh(X, Y, Z,
                       norm=colors.SymLogNorm(linthresh=0.03, linscale=0.03,
                                              vmin=-1.0, vmax=1.0, base=10),
                       cmap='RdBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='both')

pcm = ax[1].pcolormesh(X, Y, Z, cmap='RdBu_r', vmin=-np.max(Z), shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='both')
plt.show()

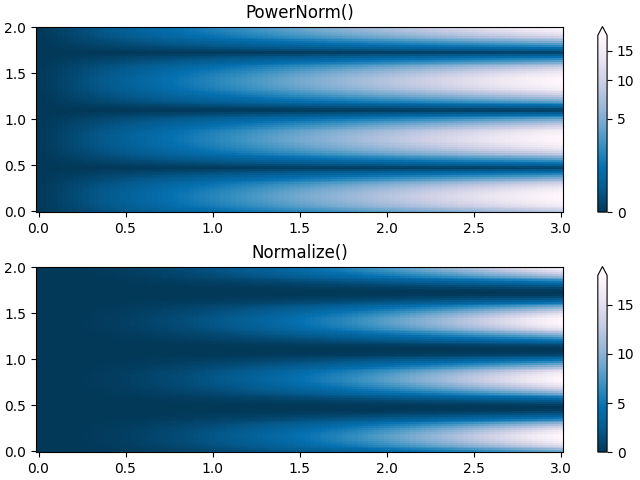
Ley de potencia

A veces es útil reasignar los colores en una relación de ley de potencia (es decir,\(y=x^{\gamma}\), dónde\(\gamma\)es el poder). Para esto usamos el colors.PowerNorm. Toma como argumento gamma ( gamma == 1.0 solo producirá la normalización lineal predeterminada):

Nota

Probablemente debería haber una buena razón para graficar los datos usando este tipo de transformación. Los espectadores técnicos están acostumbrados a ejes lineales y logarítmicos y transformaciones de datos. Las leyes de potencia son menos comunes, y los espectadores deben saber explícitamente que se han utilizado.

N = 100
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2

fig, ax = plt.subplots(2, 1, constrained_layout=True)

pcm = ax[0].pcolormesh(X, Y, Z1, norm=colors.PowerNorm(gamma=0.5),
                       cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='max')
ax[0].set_title('PowerNorm()')

pcm = ax[1].pcolormesh(X, Y, Z1, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='max')
ax[1].set_title('Normalize()')
plt.show()

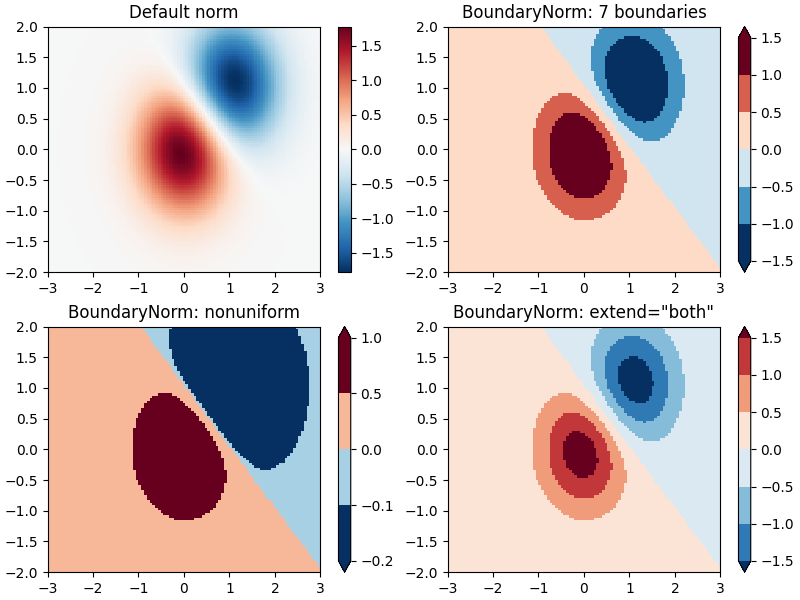
Límites discretos

Otra normalización que viene con Matplotlib es colors.BoundaryNorm. Además de vmin y vmax , esto toma como argumentos los límites entre los cuales se mapearán los datos. Luego, los colores se distribuyen linealmente entre estos "límites". También puede tomar un argumento de extensión para agregar valores fuera de los límites superiores y/o inferiores al rango en el que se distribuyen los colores. Por ejemplo:

In [4]: import matplotlib.colors as colors

In [5]: bounds = np.array([-0.25, -0.125, 0, 0.5, 1])

In [6]: norm = colors.BoundaryNorm(boundaries=bounds, ncolors=4)

In [7]: print(norm([-0.2, -0.15, -0.02, 0.3, 0.8, 0.99]))
[0 0 1 2 3 3]

Nota: A diferencia de las otras normas, esta norma devuelve valores de 0 a ncolors -1.

N = 100
X, Y = np.meshgrid(np.linspace(-3, 3, N), np.linspace(-2, 2, N))
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = ((Z1 - Z2) * 2)[:-1, :-1]

fig, ax = plt.subplots(2, 2, figsize=(8, 6), constrained_layout=True)
ax = ax.flatten()

# Default norm:
pcm = ax[0].pcolormesh(X, Y, Z, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[0], orientation='vertical')
ax[0].set_title('Default norm')

# Even bounds give a contour-like effect:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[1].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[1], extend='both', orientation='vertical')
ax[1].set_title('BoundaryNorm: 7 boundaries')

# Bounds may be unevenly spaced:
bounds = np.array([-0.2, -0.1, 0, 0.5, 1])
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[2].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[2], extend='both', orientation='vertical')
ax[2].set_title('BoundaryNorm: nonuniform')

# With out-of-bounds colors:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256, extend='both')
pcm = ax[3].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
# The colorbar inherits the "extend" argument from BoundaryNorm.
fig.colorbar(pcm, ax=ax[3], orientation='vertical')
ax[3].set_title('BoundaryNorm: extend="both"')
plt.show()

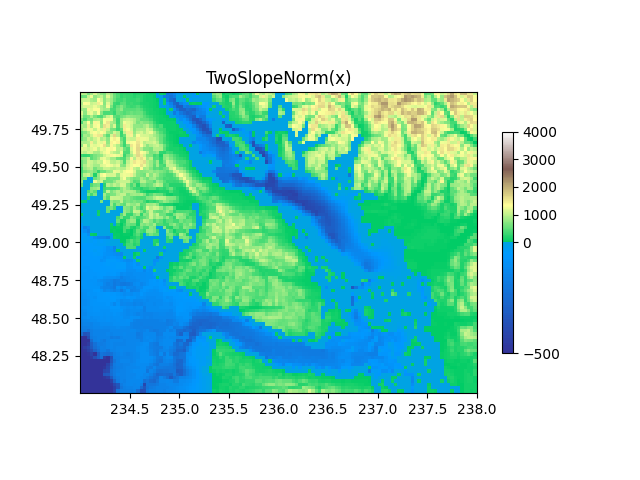
TwoSlopeNorm: mapeo diferente a cada lado de un centro

A veces queremos tener un mapa de colores diferente a cada lado de un punto central conceptual y queremos que esos dos mapas de colores tengan escalas lineales diferentes. Un ejemplo es un mapa topográfico en el que la tierra y el océano tienen un centro en cero, pero la tierra normalmente tiene un rango de elevación mayor que el rango de profundidad del agua y, a menudo, se representan con un mapa de color diferente.

dem = cbook.get_sample_data('topobathy.npz', np_load=True)
topo = dem['topo']
longitude = dem['longitude']
latitude = dem['latitude']

fig, ax = plt.subplots()
# make a colormap that has land and ocean clearly delineated and of the
# same length (256 + 256)
colors_undersea = plt.cm.terrain(np.linspace(0, 0.17, 256))
colors_land = plt.cm.terrain(np.linspace(0.25, 1, 256))
all_colors = np.vstack((colors_undersea, colors_land))
terrain_map = colors.LinearSegmentedColormap.from_list(
    'terrain_map', all_colors)

# make the norm:  Note the center is offset so that the land has more
# dynamic range:
divnorm = colors.TwoSlopeNorm(vmin=-500., vcenter=0, vmax=4000)

pcm = ax.pcolormesh(longitude, latitude, topo, rasterized=True, norm=divnorm,
                    cmap=terrain_map, shading='auto')
# Simple geographic plot, set aspect ratio because distance between lines of
# longitude depends on latitude.
ax.set_aspect(1 / np.cos(np.deg2rad(49)))
ax.set_title('TwoSlopeNorm(x)')
cb = fig.colorbar(pcm, shrink=0.6)
cb.set_ticks([-500, 0, 1000, 2000, 3000, 4000])
plt.show()

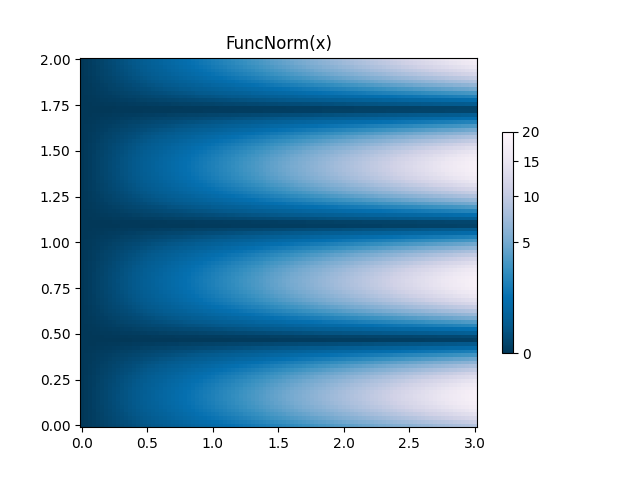
FuncNorm: normalización de función arbitraria

Si las normas anteriores no proporcionan la normalización que desea, puede utilizarlas FuncNormpara definir la suya propia. Tenga en cuenta que este ejemplo es el mismo que PowerNormcon una potencia de 0,5:

def _forward(x):
    return np.sqrt(x)


def _inverse(x):
    return x**2

N = 100
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2
fig, ax = plt.subplots()

norm = colors.FuncNorm((_forward, _inverse), vmin=0, vmax=20)
pcm = ax.pcolormesh(X, Y, Z1, norm=norm, cmap='PuBu_r', shading='auto')
ax.set_title('FuncNorm(x)')
fig.colorbar(pcm, shrink=0.6)
plt.show()

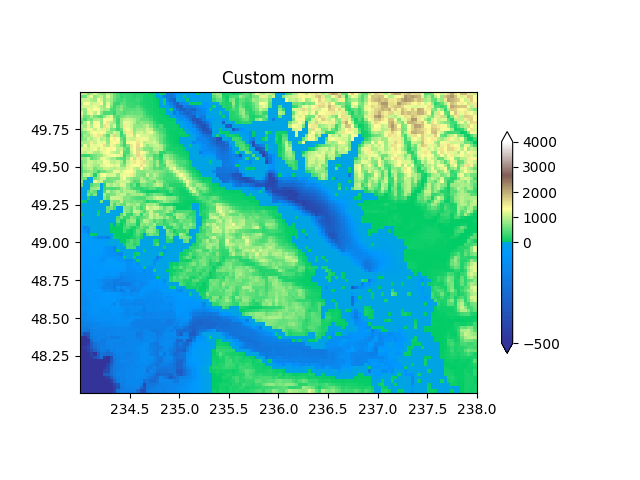
Normalización personalizada: implementar manualmente dos rangos lineales

Lo TwoSlopeNormdescrito anteriormente es un ejemplo útil para definir su propia norma. Tenga en cuenta que para que la barra de colores funcione, debe definir un inverso para su norma:

class MidpointNormalize(colors.Normalize):
    def __init__(self, vmin=None, vmax=None, vcenter=None, clip=False):
        self.vcenter = vcenter
        super().__init__(vmin, vmax, clip)

    def __call__(self, value, clip=None):
        # I'm ignoring masked values and all kinds of edge cases to make a
        # simple example...
        # Note also that we must extrapolate beyond vmin/vmax
        x, y = [self.vmin, self.vcenter, self.vmax], [0, 0.5, 1.]
        return np.ma.masked_array(np.interp(value, x, y,
                                            left=-np.inf, right=np.inf))

    def inverse(self, value):
        y, x = [self.vmin, self.vcenter, self.vmax], [0, 0.5, 1]
        return np.interp(value, x, y, left=-np.inf, right=np.inf)


fig, ax = plt.subplots()
midnorm = MidpointNormalize(vmin=-500., vcenter=0, vmax=4000)

pcm = ax.pcolormesh(longitude, latitude, topo, rasterized=True, norm=midnorm,
                    cmap=terrain_map, shading='auto')
ax.set_aspect(1 / np.cos(np.deg2rad(49)))
ax.set_title('Custom norm')
cb = fig.colorbar(pcm, shrink=0.6, extend='both')
cb.set_ticks([-500, 0, 1000, 2000, 3000, 4000])

plt.show()