Tutorial de Transformaciones

Al igual que cualquier paquete de gráficos, Matplotlib se basa en un marco de transformación para moverse fácilmente entre los sistemas de coordenadas, el sistema de coordenadas de datos del área de usuario, el sistema de coordenadas de ejes , el sistema de coordenadas de figuras y el sistema de coordenadas de visualización . En el 95% de su trazado, no necesitará pensar en esto, ya que sucede bajo el capó, pero a medida que supera los límites de la generación de figuras personalizadas, es útil comprender estos objetos para que pueda reutilizar el existente. transformaciones que Matplotlib pone a su disposición, o cree las suyas propias (ver matplotlib.transforms). La siguiente tabla resume algunos sistemas de coordenadas útiles, una descripción de cada sistema y el objeto de transformación para pasar de cada sistema de coordenadas almostrar coordenadas. En la columna "Objeto de transformación", axes una Axesinstancia, figes una Figureinstancia y subfigurees una SubFigureinstancia.

Sistema coordinado	Descripción	Objeto de transformación de sistema a pantalla
"datos"	El sistema de coordenadas de los datos en los ejes.	ax.transData
"hachas"	El sistema de coordenadas del Axes; (0, 0) está en la parte inferior izquierda de los ejes y (1, 1) está en la parte superior derecha de los ejes.	ax.transAxes
"subfigura"	El sistema de coordenadas del SubFigure; (0, 0) está en la parte inferior izquierda de la subfigura y (1, 1) está en la parte superior derecha de la subfigura. Si una figura no tiene subfiguras, esto es lo mismo que transFigure.	subfigure.transSubfigure
"figura"	El sistema de coordenadas del Figure; (0, 0) está en la parte inferior izquierda de la figura y (1, 1) está en la parte superior derecha de la figura.	fig.transFigure
"figura-pulgadas"	El sistema de coordenadas del Figureen pulgadas; (0, 0) es la parte inferior izquierda de la figura y (ancho, alto) es la parte superior derecha de la figura en pulgadas.	fig.dpi_scale_trans
"ejex", "ejey"	Sistemas de coordenadas combinados, utilizando coordenadas de datos en una dirección y coordenadas de ejes en la otra.	ax.get_xaxis_transform(), ax.get_yaxis_transform()
"monitor"	El sistema de coordenadas nativo de la salida; (0, 0) es la parte inferior izquierda de la ventana y (ancho, alto) es la parte superior derecha de la salida en "unidades de visualización". La interpretación exacta de las unidades depende del back-end. Por ejemplo, son píxeles para Agg y puntos para svg/pdf.	None, o IdentityTransform()

Los Transformobjetos son ingenuos para los sistemas de coordenadas de origen y destino, sin embargo, los objetos a los que se hace referencia en la tabla anterior están construidos para tomar entradas en su sistema de coordenadas y transformar la entrada al sistema de coordenadas de visualización . Es por eso que el sistema de coordenadas de visualizaciónNone tiene para la columna "Objeto de transformación": ya está en las coordenadas de visualización . Las convenciones de nomenclatura y destino son una ayuda para realizar un seguimiento de los sistemas de coordenadas y transformaciones "estándar" disponibles.

Las transformaciones también saben cómo invertirse (mediante Transform.inverted) para generar una transformación del sistema de coordenadas de salida al sistema de coordenadas de entrada. Por ejemplo, ax.transDataconvierte valores en coordenadas de datos a coordenadas de visualización y ax.transData.inversed()es un matplotlib.transforms.Transformque va de coordenadas de visualización a coordenadas de datos. Esto es particularmente útil cuando se procesan eventos desde la interfaz de usuario, que generalmente ocurren en el espacio de visualización, y desea saber dónde se produjo el clic del mouse o la tecla presionada en su sistema de coordenadas de datos .

Tenga en cuenta que especificar la posición de los artistas en las coordenadas de visualización puede cambiar su ubicación relativa si dpicambia el tamaño de la figura. Esto puede causar confusión al imprimir o cambiar la resolución de la pantalla, porque el objeto puede cambiar de ubicación y tamaño. Por lo tanto, es más común que los artistas colocados en ejes o figuras tengan su transformación configurada en algo diferente al IdentityTransform(); el valor predeterminado cuando se agrega un artista a un Axes usando add_artistes que la transformación sea ax.transDatapara que pueda trabajar y pensar en coordenadas de datos y dejar que Matplotlib se encargue de la transformación para mostrar .

Coordenadas de datos

Comencemos con la coordenada más utilizada, el sistema de coordenadas de datos . Cada vez que agrega datos a los ejes, Matplotlib actualiza los límites de datos, más comúnmente actualizados con los métodos set_xlim()y . set_ylim()Por ejemplo, en la siguiente figura, los límites de datos se extienden de 0 a 10 en el eje x y de -1 a 1 en el eje y.

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches

x = np.arange(0, 10, 0.005)
y = np.exp(-x/2.) * np.sin(2*np.pi*x)

fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_xlim(0, 10)
ax.set_ylim(-1, 1)

plt.show()

Puede usar la ax.transDatainstancia para transformar sus datos en su sistema de coordenadas de visualización , ya sea un solo punto o una secuencia de puntos, como se muestra a continuación:

In [14]: type(ax.transData)
Out[14]: <class 'matplotlib.transforms.CompositeGenericTransform'>

In [15]: ax.transData.transform((5, 0))
Out[15]: array([ 335.175,  247.   ])

In [16]: ax.transData.transform([(5, 0), (1, 2)])
Out[16]:
array([[ 335.175,  247.   ],
       [ 132.435,  642.2  ]])

Puede usar el inverted() método para crear una transformación que lo llevará de la visualización a las coordenadas de datos :

In [41]: inv = ax.transData.inverted()

In [42]: type(inv)
Out[42]: <class 'matplotlib.transforms.CompositeGenericTransform'>

In [43]: inv.transform((335.175,  247.))
Out[43]: array([ 5.,  0.])

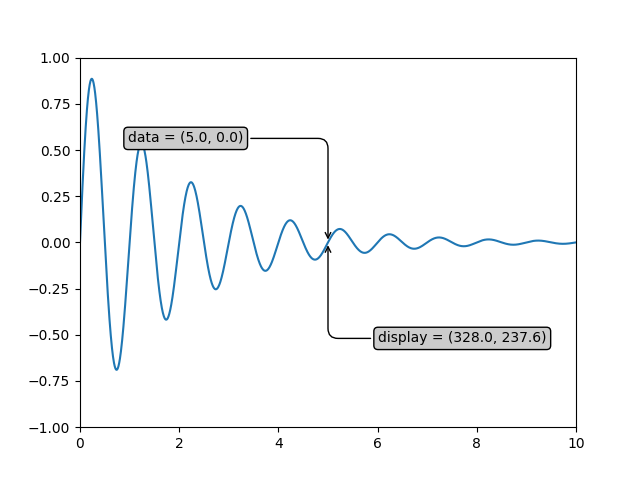
Si está escribiendo junto con este tutorial, los valores exactos de las coordenadas de visualización pueden diferir si tiene un tamaño de ventana diferente o una configuración de ppp. Del mismo modo, en la figura a continuación, los puntos etiquetados de visualización probablemente no sean los mismos que en la sesión de ipython porque los valores predeterminados de tamaño de la figura de la documentación son diferentes.

x = np.arange(0, 10, 0.005)
y = np.exp(-x/2.) * np.sin(2*np.pi*x)

fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_xlim(0, 10)
ax.set_ylim(-1, 1)

xdata, ydata = 5, 0
# This computing the transform now, if anything
# (figure size, dpi, axes placement, data limits, scales..)
# changes re-calling transform will get a different value.
xdisplay, ydisplay = ax.transData.transform((xdata, ydata))

bbox = dict(boxstyle="round", fc="0.8")
arrowprops = dict(
    arrowstyle="->",
    connectionstyle="angle,angleA=0,angleB=90,rad=10")

offset = 72
ax.annotate('data = (%.1f, %.1f)' % (xdata, ydata),
            (xdata, ydata), xytext=(-2*offset, offset), textcoords='offset points',
            bbox=bbox, arrowprops=arrowprops)

disp = ax.annotate('display = (%.1f, %.1f)' % (xdisplay, ydisplay),
                   (xdisplay, ydisplay), xytext=(0.5*offset, -offset),
                   xycoords='figure pixels',
                   textcoords='offset points',
                   bbox=bbox, arrowprops=arrowprops)

plt.show()

Advertencia

Si ejecuta el código fuente en el ejemplo anterior en un backend de GUI, también puede encontrar que las dos flechas para los datos y las anotaciones de visualización no apuntan exactamente al mismo punto. Esto se debe a que el punto de visualización se calculó antes de que se mostrara la figura, y el backend de la GUI puede cambiar ligeramente el tamaño de la figura cuando se crea. El efecto es más pronunciado si cambias el tamaño de la figura tú mismo. Esta es una buena razón por la que rara vez desea trabajar en el espacio de visualización , pero puede conectarse a 'on_draw' Eventpara actualizar las coordenadas de las figuras en los dibujos de figuras; véase Manejo de eventos y selección .

Cuando cambia los límites x o y de sus ejes, los límites de datos se actualizan para que la transformación produzca un nuevo punto de visualización. Tenga en cuenta que cuando solo cambiamos el ylim, solo se modifica la coordenada de visualización y, y cuando también cambiamos el xlim, ambos se modifican. Más sobre esto más adelante cuando hablemos del Bbox.

In [54]: ax.transData.transform((5, 0))
Out[54]: array([ 335.175,  247.   ])

In [55]: ax.set_ylim(-1, 2)
Out[55]: (-1, 2)

In [56]: ax.transData.transform((5, 0))
Out[56]: array([ 335.175     ,  181.13333333])

In [57]: ax.set_xlim(10, 20)
Out[57]: (10, 20)

In [58]: ax.transData.transform((5, 0))
Out[58]: array([-171.675     ,  181.13333333])

Coordenadas de los ejes

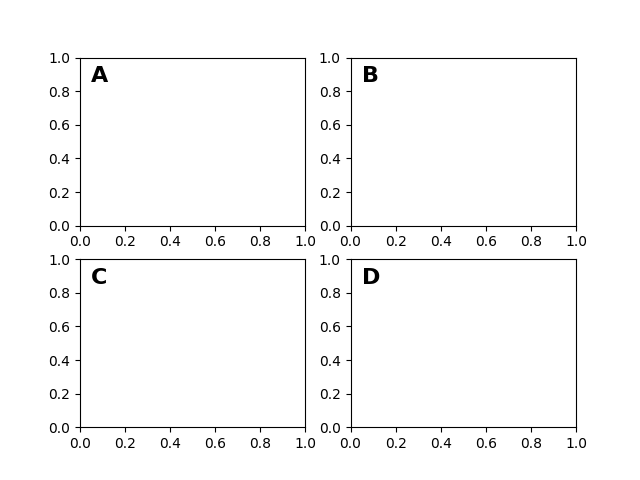
Después del sistema de coordenadas de datos , los ejes son probablemente el segundo sistema de coordenadas más útil. Aquí el punto (0, 0) es la parte inferior izquierda de sus ejes o subparcela, (0.5, 0.5) es el centro y (1.0, 1.0) es la parte superior derecha. También puede referirse a puntos fuera del rango, por lo que (-0.1, 1.1) está a la izquierda y arriba de sus ejes. Este sistema de coordenadas es extremadamente útil al colocar texto en sus ejes, porque a menudo desea una burbuja de texto en una ubicación fija, por ejemplo, la parte superior izquierda del panel de ejes, y que esa ubicación permanezca fija cuando realiza una panorámica o hace zoom. Aquí hay un ejemplo simple que crea cuatro paneles y los etiqueta 'A', 'B', 'C', 'D' como se ve a menudo en las revistas.

fig = plt.figure()
for i, label in enumerate(('A', 'B', 'C', 'D')):
    ax = fig.add_subplot(2, 2, i+1)
    ax.text(0.05, 0.95, label, transform=ax.transAxes,
            fontsize=16, fontweight='bold', va='top')

plt.show()

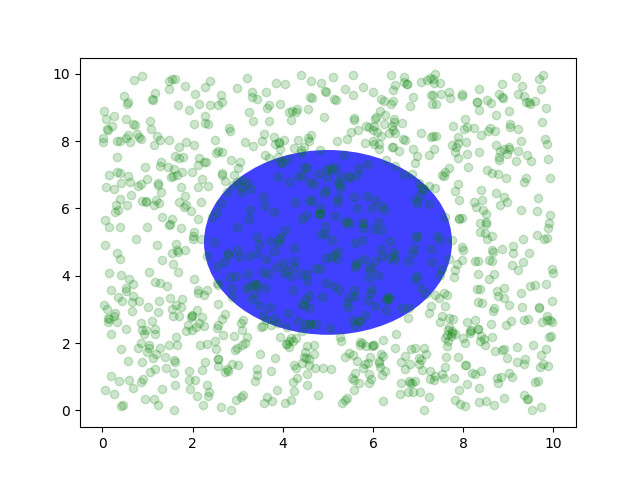
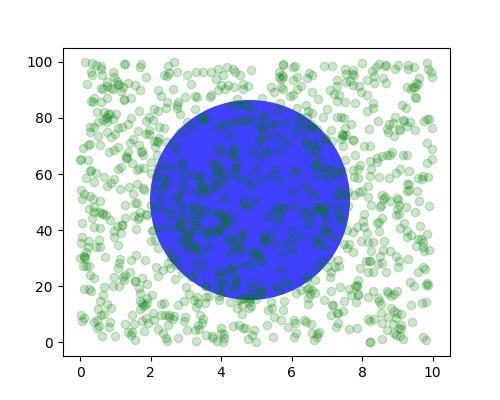
También puede hacer líneas o parches en el sistema de coordenadas de ejes , pero en mi experiencia, esto es menos útil que usarlo ax.transAxespara colocar texto. No obstante, aquí hay un ejemplo tonto que traza algunos puntos aleatorios en el espacio de datos y superpone un centro semitransparente Circleen el medio de los ejes con un radio de una cuarta parte de los ejes, si sus ejes no conservan la relación de aspecto (ver set_aspect()) , esto se verá como una elipse. Use la herramienta de panorámica/zoom para moverse, o cambie manualmente los datos xlim e ylim, y verá que los datos se mueven, pero el círculo permanecerá fijo porque no está en las coordenadas de los datos y siempre permanecerá en el centro de los ejes. .

fig, ax = plt.subplots()
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y, 'go', alpha=0.2)  # plot some data in data coordinates

circ = mpatches.Circle((0.5, 0.5), 0.25, transform=ax.transAxes,
                       facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()

Transformaciones combinadas

Dibujar en espacios de coordenadas combinadas que mezclen ejes con coordenadas de datos es extremadamente útil, por ejemplo, para crear un tramo horizontal que resalte alguna región de los datos y pero se extienda a lo largo del eje x independientemente de los límites de datos, el nivel de panorámica o zoom, etc. De hecho, estas líneas y tramos combinados son tan útiles que hemos incorporado funciones para que sean fáciles de trazar (consulte axhline(), axvline(), axhspan(), axvspan()) pero, con fines didácticos, implementaremos el tramo horizontal aquí usando una transformación combinada. Este truco solo funciona para transformaciones separables, como las que se ven en los sistemas de coordenadas cartesianas normales, pero no en transformaciones inseparables como el PolarTransform.

import matplotlib.transforms as transforms

fig, ax = plt.subplots()
x = np.random.randn(1000)

ax.hist(x, 30)
ax.set_title(r'$\sigma=1 \/ \dots \/ \sigma=2$', fontsize=16)

# the x coords of this transformation are data, and the y coord are axes
trans = transforms.blended_transform_factory(
    ax.transData, ax.transAxes)
# highlight the 1..2 stddev region with a span.
# We want x to be in data coordinates and y to span from 0..1 in axes coords.
rect = mpatches.Rectangle((1, 0), width=1, height=1, transform=trans,
                          color='yellow', alpha=0.5)
ax.add_patch(rect)

plt.show()

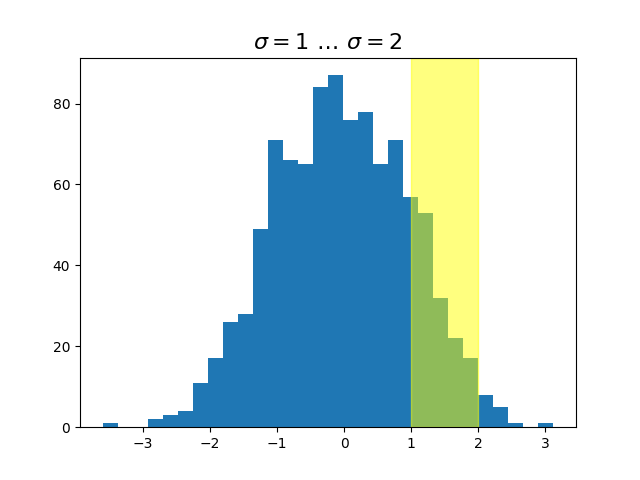
Nota

Las transformaciones combinadas donde x está en coordenadas de datos e y en coordenadas de ejes son tan útiles que tenemos métodos auxiliares para devolver las versiones que Matplotlib usa internamente para dibujar marcas, etiquetas de marcas, etc. Los métodos son matplotlib.axes.Axes.get_xaxis_transform()y matplotlib.axes.Axes.get_yaxis_transform(). Entonces, en el ejemplo anterior, la llamada a blended_transform_factory()puede ser reemplazada por get_xaxis_transform:

trans = ax.get_xaxis_transform()

Trazado en coordenadas físicas

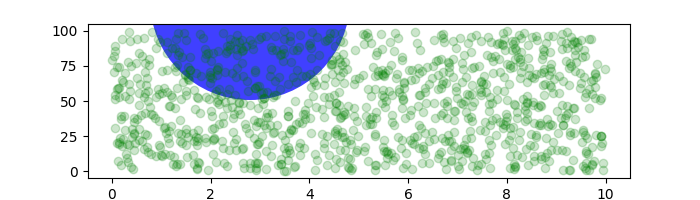
A veces queremos que un objeto tenga cierto tamaño físico en la trama. Aquí dibujamos el mismo círculo que arriba, pero en coordenadas físicas. Si se hace de forma interactiva, puede ver que cambiar el tamaño de la figura no cambia el desplazamiento del círculo desde la esquina inferior izquierda, no cambia su tamaño y el círculo sigue siendo un círculo independientemente de la relación de aspecto de los ejes.

fig, ax = plt.subplots(figsize=(5, 4))
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y*10., 'go', alpha=0.2)  # plot some data in data coordinates
# add a circle in fixed-coordinates
circ = mpatches.Circle((2.5, 2), 1.0, transform=fig.dpi_scale_trans,
                       facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()

Si cambiamos el tamaño de la figura, el círculo no cambia su posición absoluta y se recorta.

fig, ax = plt.subplots(figsize=(7, 2))
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y*10., 'go', alpha=0.2)  # plot some data in data coordinates
# add a circle in fixed-coordinates
circ = mpatches.Circle((2.5, 2), 1.0, transform=fig.dpi_scale_trans,
                       facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()

Otro uso es colocar un parche con una dimensión física establecida alrededor de un punto de datos en los ejes. Aquí sumamos dos transformaciones. El primero establece la escala de cuán grande debe ser la elipse y el segundo establece su posición. Luego, la elipse se coloca en el origen y luego usamos la transformación auxiliar ScaledTranslation para moverla al lugar correcto en el ax.transDatasistema de coordenadas. Este ayudante se instancia con:

trans = ScaledTranslation(xt, yt, scale_trans)

donde xt e yt son las compensaciones de traducción, y scale_trans es una transformación que escala xt e yt en el momento de la transformación antes de aplicar las compensaciones.

Tenga en cuenta el uso del operador más en las transformaciones a continuación. Este código dice: primero aplique la transformación de escala fig.dpi_scale_trans para hacer que la elipse tenga el tamaño adecuado, pero aún centrada en (0, 0), y luego traduzca los datos al espacio xdata[0]de ydata[0]datos.

En uso interactivo, la elipse permanece del mismo tamaño incluso si los límites de los ejes se cambian mediante el zoom.

fig, ax = plt.subplots()
xdata, ydata = (0.2, 0.7), (0.5, 0.5)
ax.plot(xdata, ydata, "o")
ax.set_xlim((0, 1))

trans = (fig.dpi_scale_trans +
         transforms.ScaledTranslation(xdata[0], ydata[0], ax.transData))

# plot an ellipse around the point that is 150 x 130 points in diameter...
circle = mpatches.Ellipse((0, 0), 150/72, 130/72, angle=40,
                          fill=None, transform=trans)
ax.add_patch(circle)
plt.show()

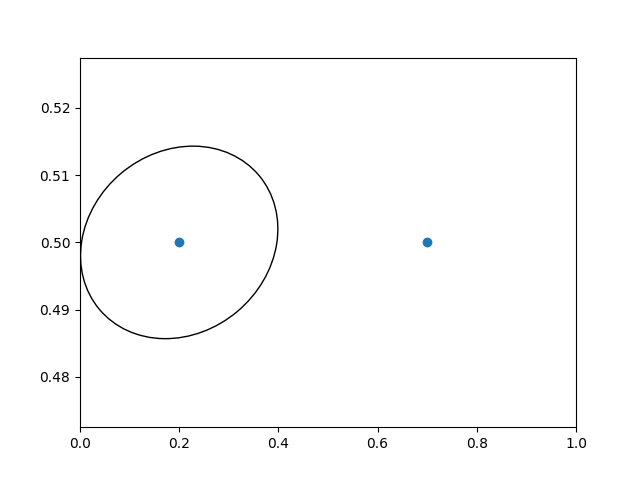
Nota

El orden de transformación importa. Aquí, la elipse recibe primero las dimensiones correctas en el espacio de visualización y luego se mueve en el espacio de datos al lugar correcto. Si hubiéramos hecho lo ScaledTranslationprimero, entonces xdata[0]y ydata[0]primero se transformaría para mostrar coordenadas ( en un monitor de 200 ppp) y luego esas coordenadas se escalarían empujando el centro de la elipse fuera de la pantalla (es decir, ).[ 358.4  475.2]fig.dpi_scale_trans[ 71680.  95040.]

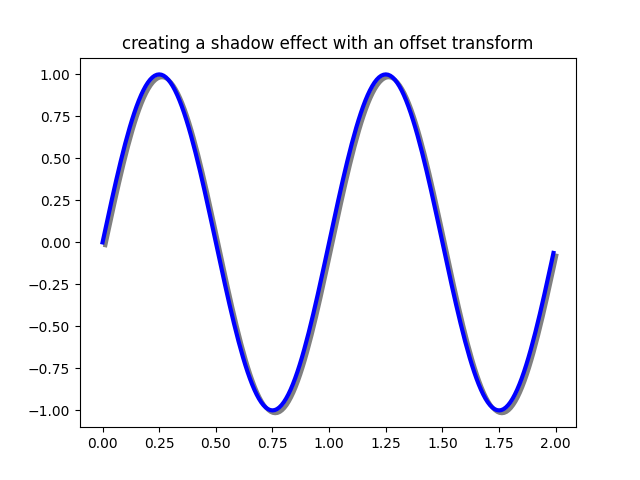
Uso de transformaciones compensadas para crear un efecto de sombra

Otro uso de ScaledTranslationes crear una nueva transformación que se desplace de otra transformación, por ejemplo, para colocar un objeto desplazado un poco con respecto a otro objeto. Por lo general, desea que el cambio sea en alguna dimensión física, como puntos o pulgadas en lugar de coordenadas de datos , para que el efecto de cambio sea constante en diferentes niveles de zoom y configuraciones de ppp.

Un uso para un desplazamiento es crear un efecto de sombra, donde dibuja un objeto idéntico al primero justo a la derecha y justo debajo de él, ajustando el zorder para asegurarse de que la sombra se dibuje primero y luego el objeto. sombreado por encima de él.

Aquí aplicamos las transformaciones en el orden opuesto al uso ScaledTranslationanterior. El gráfico se hace primero en coordenadas de datos ( ax.transData) y luego se desplaza por dxy dypuntos usando fig.dpi_scale_trans. (En tipografía, un punto es 1/72 pulgadas, y al especificar sus desplazamientos en puntos, su figura se verá igual independientemente de la resolución de dpi en la que se guarde).

fig, ax = plt.subplots()

# make a simple sine wave
x = np.arange(0., 2., 0.01)
y = np.sin(2*np.pi*x)
line, = ax.plot(x, y, lw=3, color='blue')

# shift the object over 2 points, and down 2 points
dx, dy = 2/72., -2/72.
offset = transforms.ScaledTranslation(dx, dy, fig.dpi_scale_trans)
shadow_transform = ax.transData + offset

# now plot the same data with our offset transform;
# use the zorder to make sure we are below the line
ax.plot(x, y, lw=3, color='gray',
        transform=shadow_transform,
        zorder=0.5*line.get_zorder())

ax.set_title('creating a shadow effect with an offset transform')
plt.show()

Nota

El desplazamiento de ppp y pulgadas es un caso de uso bastante común en el que tenemos una función auxiliar especial para crearlo matplotlib.transforms.offset_copy(), que devuelve una nueva transformación con un desplazamiento agregado. Así que arriba podríamos haber hecho:

shadow_transform = transforms.offset_copy(ax.transData,
         fig=fig, dx, dy, units='inches')

La tubería de transformación

La ax.transDatatransformación con la que hemos estado trabajando en este tutorial es un compuesto de tres transformaciones diferentes que comprenden la canalización de transformación de datos -> visualización coordenadas Michael Droettboom implementó el marco de transformaciones, teniendo cuidado de proporcionar una API limpia que separó las proyecciones y escalas no lineales que ocurren en gráficos polares y logarítmicos, de las transformaciones afines lineales que ocurren cuando se desplaza y se acerca. Hay una eficiencia aquí, porque puede desplazarse y hacer zoom en sus ejes, lo que afecta la transformación afín, pero es posible que no necesite calcular las proyecciones o escalas no lineales potencialmente costosas en eventos de navegación simples. También es posible multiplicar matrices de transformación afines y luego aplicarlas a las coordenadas en un solo paso. Esto no es cierto para todas las transformaciones posibles.

Así es como ax.transDatase define la instancia en la clase básica de eje separable Axes:

self.transData = self.transScale + (self.transLimits + self.transAxes)

Hemos sido presentados a la transAxesinstancia anterior en Coordenadas de ejes , que mapea las esquinas (0, 0), (1, 1) de los ejes o el cuadro delimitador de la subparcela para mostrar el espacio, así que veamos estas otras dos piezas.

self.transLimitses la transformación que te lleva de datos a coordenadas de ejes ; es decir, asigna su vista xlim e ylim a la unidad de espacio de los ejes (y transAxesluego toma esa unidad de espacio para mostrar el espacio). Podemos ver esto en acción aquí

In [80]: ax = plt.subplot()

In [81]: ax.set_xlim(0, 10)
Out[81]: (0, 10)

In [82]: ax.set_ylim(-1, 1)
Out[82]: (-1, 1)

In [84]: ax.transLimits.transform((0, -1))
Out[84]: array([ 0.,  0.])

In [85]: ax.transLimits.transform((10, -1))
Out[85]: array([ 1.,  0.])

In [86]: ax.transLimits.transform((10, 1))
Out[86]: array([ 1.,  1.])

In [87]: ax.transLimits.transform((5, 0))
Out[87]: array([ 0.5,  0.5])

y podemos usar esta misma transformación invertida para pasar de las coordenadas de los ejes unitarios a las coordenadas de los datos .

In [90]: inv.transform((0.25, 0.25))
Out[90]: array([ 2.5, -0.5])

La pieza final es el self.transScaleatributo, que es responsable de la escala no lineal opcional de los datos, por ejemplo, para ejes logarítmicos. Cuando se configura inicialmente un eje, solo se establece en la transformación de identidad, ya que los ejes básicos de Matplotlib tienen una escala lineal, pero cuando llama a una función de escala logarítmica como semilogx()o establece explícitamente la escala en logarítmica con set_xscale(), entonces el ax.transScaleatributo se establece para manejar la proyección no lineal. Las transformadas de escala son propiedades de las respectivas xaxisinstancias yaxis Axis. Por ejemplo, cuando llama a ax.set_xscale('log'), el eje x actualiza su escala a una matplotlib.scale.LogScaleinstancia.

Para los ejes no separables PolarAxes, hay una pieza más a considerar, la transformación de proyección. Es transData matplotlib.projections.polar.PolarAxessimilar al de los típicos ejes matplotlib separables, con una pieza adicional transProjection:

self.transData = self.transScale + self.transProjection + \
    (self.transProjectionAffine + self.transAxes)

transProjectionmaneja la proyección desde el espacio, por ejemplo, latitud y longitud para datos de mapas, o radio y theta para datos polares, a un sistema de coordenadas cartesianas separables. Hay varios ejemplos de proyección en el matplotlib.projectionspaquete, y la mejor manera de obtener más información es abrir el código fuente de esos paquetes y ver cómo crear uno propio, ya que Matplotlib admite proyecciones y ejes extensibles. Michael Droettboom ha proporcionado un buen ejemplo de tutorial sobre la creación de ejes de proyección Hammer; consulte Proyección personalizada .