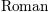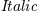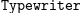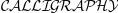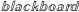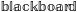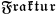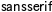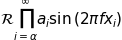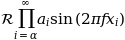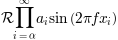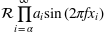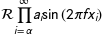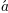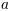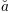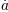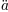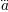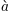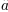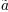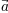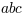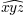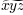Escritura de expresiones matemáticas

Puede usar un subconjunto de marcado TeX en cualquier cadena de texto de Matplotlib colocándolo dentro de un par de signos de dólar ($).

Tenga en cuenta que no necesita tener TeX instalado, ya que Matplotlib incluye su propio analizador de expresiones TeX, motor de diseño y fuentes. El motor de diseño es una adaptación bastante directa de los algoritmos de diseño en TeX de Donald Knuth, por lo que la calidad es bastante buena (Matplotlib también ofrece una usetex opción para aquellos que quieren llamar a TeX para generar su texto; consulte Representación de texto con LaTeX ) .

Cualquier elemento de texto puede usar texto matemático. Debe usar cadenas sin procesar (preceda las comillas con un 'r') y rodee el texto matemático con signos de dólar ($), como en TeX. El texto regular y el texto matemático se pueden intercalar dentro de la misma cadena. Mathtext puede usar DejaVu Sans (predeterminado), DejaVu Serif, las fuentes Computer Modern (de (La)TeX), fuentes STIX (que están diseñadas para combinarse bien con Times) o una fuente Unicode que usted proporcione. La fuente del texto matemático se puede seleccionar a través rcParams["mathtext.fontset"]de (predeterminado :) 'dejavusans'(consulte Personalización de Matplotlib con hojas de estilo y rcParams )

Aquí hay un ejemplo simple:

# plain text
plt.title('alpha > beta')

produce "alfa > beta".

Considerando que esto:

# math text
plt.title(r'$\alpha > \beta$')

produce " ".

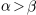Nota

Mathtext debe colocarse entre un par de signos de dólar ($). Para facilitar la visualización de valores monetarios, por ejemplo, "$100,00", si un solo signo de dólar está presente en toda la cadena, se mostrará textualmente como un signo de dólar. Este es un pequeño cambio con respecto a TeX normal, donde el signo de dólar en texto no matemático tendría que escaparse ('\$').

Nota

Mientras que la sintaxis dentro del par de signos de dólar ($) pretende ser similar a TeX, el texto exterior no. En particular, personajes como:

# $ % & ~ _ ^ \ { } \( \) \[ \]

tienen un significado especial fuera del modo matemático en TeX. Por lo tanto, estos caracteres se comportarán de manera diferente dependiendo de rcParams["text.usetex"](predeterminado: False). Consulte el tutorial de usetex para obtener más información.

Subíndices y superíndices

Para hacer subíndices y superíndices, use los símbolos '_'y :'^'

r'$\alpha_i > \beta_i$'

\[\alpha_i > \beta_i\]

Para mostrar subíndices o superíndices de varias letras correctamente, debe ponerlos entre llaves {...}:

r'$\alpha^{ic} > \beta_{ic}$'

\[\alpha^{ic} > \beta_{ic}\]

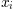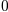Algunos símbolos colocan automáticamente sus sub/superíndices debajo y sobre el operador. Por ejemplo, para escribir la suma de from to 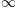, podrías hacer:

r'$\sum_{i=0}^\infty x_i$'

\[\sum_{i=0}^\infty x_i\]

Fracciones, binomios y números apilados

Se pueden crear fracciones, binomios y números apilados con los comandos y \frac{}{}, respectivamente:\binom{}{}\genfrac{}{}{}{}{}{}

r'$\frac{3}{4} \binom{3}{4} \genfrac{}{}{0}{}{3}{4}$'

produce

\[\frac{3}{4} \binom{3}{4} \genfrac{}{}{0pt}{}{3}{4}\]

Las fracciones se pueden anidar arbitrariamente:

r'$\frac{5 - \frac{1}{x}}{4}$'

produce

\[\frac{5 - \frac{1}{x}}{4}\]

Tenga en cuenta que se debe tener especial cuidado al colocar paréntesis y corchetes alrededor de las fracciones. Hacer las cosas de la manera obvia produce paréntesis que son demasiado pequeños:

r'$(\frac{5 - \frac{1}{x}}{4})$'

\[(\frac{5 - \frac{1}{x}}{4})\]

La solución es anteponer el corchete \lefte \rightinformar al analizador que esos corchetes abarcan todo el objeto:

r'$\left(\frac{5 - \frac{1}{x}}{4}\right)$'

\[\left(\frac{5 - \frac{1}{x}}{4}\right)\]

Radicales

Los radicales se pueden producir con el \sqrt[]{}comando. Por ejemplo:

r'$\sqrt{2}$'

\[\sqrt{2}\]

Cualquier base puede proporcionarse (opcionalmente) entre corchetes. Tenga en cuenta que la base debe ser una expresión simple y no puede contener comandos de diseño como fracciones o sub/superíndices:

r'$\sqrt[3]{x}$'

\[\sqrt[3]{x}\]

Fuentes

La fuente predeterminada es la cursiva para los símbolos matemáticos.

Nota

Este valor predeterminado se puede cambiar usando rcParams["mathtext.default"](predeterminado: 'it'). Esto es útil, por ejemplo, para usar la misma fuente que el texto normal que no es matemático para el texto matemático, configurándolo en regular.

Para cambiar las fuentes, por ejemplo, para escribir "pecado" en fuente romana, encierre el texto en un comando de fuente:

r'$s(t) = \mathcal{A}\mathrm{sin}(2 \omega t)$'

\[s(t) = \mathcal{A}\mathrm{sin}(2 \omega t)\]

Más convenientemente, muchos nombres de funciones de uso común que están escritos en una fuente romana tienen accesos directos. Entonces, la expresión anterior podría escribirse de la siguiente manera:

r'$s(t) = \mathcal{A}\sin(2 \omega t)$'

\[s(t) = \mathcal{A}\sin(2 \omega t)\]

Aquí, "s" y "t" son variables en letra cursiva (predeterminada), "sin" está en letra romana y la amplitud "A" está en letra caligráfica. Tenga en cuenta que en el ejemplo anterior, la caligrafía Aestá comprimida en el archivo sin. Puede usar un comando de espaciado para agregar un pequeño espacio en blanco entre ellos:

r's(t) = \mathcal{A}\/\sin(2 \omega t)'

\[s(t) = \mathcal{A}\,\sin(2 \omega t)\]

Las opciones disponibles con todas las fuentes son:

Dominio	Resultado
\mathrm{Roman}
\mathit{Italic}
\mathtt{Typewriter}
\mathcal{CALLIGRAPHY}

Al usar las fuentes STIX , también tiene la opción de:

Dominio	Resultado
\mathbb{blackboard}
\mathrm{\mathbb{blackboard}}
\mathfrak{Fraktur}
\mathsf{sansserif}
\mathrm{\mathsf{sansserif}}

También hay cinco "conjuntos de fuentes" globales para elegir, que se seleccionan usando el mathtext.fontsetparámetro en matplotlibrc .

dejavusans: Deja Vu Sans

dejavuserif: DejaVu Serif

cm: Computadora moderna (TeX)

stix: STIX (diseñado para combinar bien con Times)

stixsans: STIX sans-serif

Además, puede usar \mathdefault{...}o su alias \mathregular{...}para usar la fuente utilizada para el texto normal fuera del texto matemático. Hay una serie de limitaciones en este enfoque, sobre todo porque habrá muchos menos símbolos disponibles, pero puede ser útil para hacer que las expresiones matemáticas se mezclen bien con otro texto en el gráfico.

Fuentes personalizadas

mathtext también proporciona una forma de usar fuentes personalizadas para matemáticas. Este método es bastante complicado de usar y debe considerarse una característica experimental solo para usuarios pacientes. Al configurar rcParams["mathtext.fontset"](predeterminado: 'dejavusans') en custom, puede configurar los siguientes parámetros, que controlan qué archivo de fuente usar para un conjunto particular de caracteres matemáticos.

Parámetro	Corresponde a
mathtext.it	\mathit{}o cursiva por defecto
mathtext.rm	\mathrm{}romano (vertical)
mathtext.tt	\mathtt{}Máquina de escribir (monoespacio)
mathtext.bf	\mathbf{}negrita cursiva
mathtext.cal	\mathcal{}caligráfico
mathtext.sf	\mathsf{}sans-serif

Cada parámetro debe establecerse en un descriptor de fuente fontconfig (como se define en el capítulo de fuente aún por escribir).

Las fuentes utilizadas deben tener un mapeo Unicode para encontrar caracteres no latinos, como el griego. Si desea usar un símbolo matemático que no está contenido en sus fuentes personalizadas, puede establecer rcParams["mathtext.fallback"](predeterminado: 'cm') en 'cm', 'stix'o 'stixsans' que hará que el sistema de texto matemático use caracteres de una fuente alternativa siempre que no se pueda encontrar un carácter en particular en la fuente personalizada.

Tenga en cuenta que los glifos matemáticos especificados en Unicode han evolucionado con el tiempo y es posible que muchas fuentes no tengan glifos en el lugar correcto para el texto matemático.

Acentos

Un comando de acento puede preceder a cualquier símbolo para agregar un acento encima. Hay formas largas y cortas para algunos de ellos.

Dominio	Resultado
\acute ao\'a
\bar a
\breve a
\dot ao\.a
\ddot ao\''a
\dddot a
\ddddot a
\grave ao\`a
\hat ao\^a
\tilde ao\~a
\vec a
\overline{abc}

Además, hay dos acentos especiales que se ajustan automáticamente al ancho de los símbolos a continuación:

Dominio	Resultado
\widehat{xyz}
\widetilde{xyz}

Se debe tener cuidado al poner acentos en minúsculas i y j. Tenga en cuenta que a continuación \imathse utiliza para evitar el punto adicional sobre la i:

r"$\hat i\ \ \hat \imath$"

\[\hat i\ \ \hat \imath\]

Símbolos

También puede usar una gran cantidad de símbolos TeX, como en \infty, \leftarrow, \sum, \int.

Griego en minúsculas

α\alpha	β\beta	x\chi	d\delta	ϝ\digamma	ε\epsilon
η\eta	γ\gamma	yo\iota	k\kappa	λ\lambda	m\mu
v\nu	ω\omega	ϕ\phi	π\pi	ψ\psi	ρ\rho
σ\sigma	τ\tau	θ\theta	υ\upsilon	ε\varepsilon	ϰ\varkappa
φ\varphi	ϖ\varpi	ϱ\varrho	ς\varsigma	ϑ\vartheta	ξ\xi
ζ\zeta

Griego en mayúsculas

Δ\Delta	Γ\Gamma	Λ\Lambda	Ω\Omega	Φ\Phi	Π\Pi	Ψ\Psi	Σ\Sigma
Θ\Theta	Υ\Upsilon	Ξ\Xi	℧\mho	∇\nabla

hebreo

ℵ\aleph

ℶ\beth

ℸ\daleth

ℷ\gimel

delimitadores

//	[[	⇓\Downarrow	⇑\Uparrow	‖\Vert	\\backslash
↓\downarrow	⟨\langle	⌈\lceil	⌊\lfloor	⌞\llcorner	⌟\lrcorner
⟩\rangle	⌉\rceil	⌋\rfloor	⌜\ulcorner	↑\uparrow	⌝\urcorner
|\vert	{\{	|\|	}\}	]]	||

Grandes simbolos

⋂\bigcap	⋃\bigcup	⨀\bigodot	⨁\bigoplus	⨂\bigotimes	⨄\biguplus
⋁\bigvee	⋀\bigwedge	∐\coprod	∫\int	∮\oint	∏\prod
∑\sum

Nombres de funciones estándar

PR\Pr	arccos\arccos	arcsen\arcsin	arcán\arctan	argumento\arg	porque\cos
aporrear\cosh	cuna\cot	bata\coth	csc\csc	grado\deg	det\det
oscuro\dim	Exp\exp	mcd\gcd	hombre\hom	inf\inf	ker\ker
lg\lg	límite\lim	limite\liminf	limpiar\limsup	en\ln	Iniciar sesión\log
máximo\max	min\min	segundo\sec	pecado\sin	pecado\sinh	sorber\sup
broncearse\tan	bronceado\tanh

Operación binaria y símbolos de relación.

≎\Bumpeq	⋒\Cap	⋓\Cup	≑\Doteq
⨝\Join	⋐\Subset	⋑\Supset	⊩\Vdash
⊪\Vvdash	≈\approx	≊\approxeq	∗\ast
≍\asymp	϶\backepsilon	∽\backsim	⋍\backsimeq
⊼\barwedge	∵\because	≬\between	○\bigcirc
▽\bigtriangledown	△\bigtriangleup	◀\blacktriangleleft	▶\blacktriangleright
⊥\bot	⋈\bowtie	⊡\boxdot	⊟\boxminus
⊞\boxplus	⊠\boxtimes	∙\bullet	≏\bumpeq
∩\cap	⋅\cdot	∘\circ	≗\circeq
≔\coloneq	≅\cong	∪\cup	⋞\curlyeqprec
⋟\curlyeqsucc	⋎\curlyvee	⋏\curlywedge	†\dag
⊣\dashv	‡\ddag	⋄\diamond	÷\div
⋇\divideontimes	≐\doteq	≑\doteqdot	∔\dotplus
⌆\doublebarwedge	≖\eqcirc	≕\eqcolon	≂\eqsim
⪖\eqslantgtr	⪕\eqslantless	≡\equiv	≒\fallingdotseq
⌢\frown	≥\geq	≧\geqq	⩾\geqslant
≫\gg	⋙\ggg	⪺\gnapprox	≩\gneqq
⋧\gnsim	⪆\gtrapprox	⋗\gtrdot	⋛\gtreqless
⪌\gtreqqless	≷\gtrless	≳\gtrsim	∈\in
⊺\intercal	⋋\leftthreetimes	≤\leq	≦\leqq
⩽\leqslant	⪅\lessapprox	⋖\lessdot	⋚\lesseqgtr
⪋\lesseqqgtr	≶\lessgtr	≲\lesssim	≪\ll
⋘\lll	⪹\lnapprox	≨\lneqq	⋦\lnsim
⋉\ltimes	∣\mid	⊧\models	∓\mp
⊯\nVDash	⊮\nVdash	≉\napprox	≇\ncong
≠\ne	≠\neq	≠\neq	≢\nequiv
≱\ngeq	≯\ngtr	∋\ni	≰\nleq
≮\nless	∤\nmid	∉\notin	∦\nparallel
⊀\nprec	≁\nsim	⊄\nsubset	⊈\nsubseteq
⊁\nsucc	⊅\nsupset	⊉\nsupseteq	⋪\ntriangleleft
⋬\ntrianglelefteq	⋫\ntriangleright	⋭\ntrianglerighteq	⊭\nvDash
⊬\nvdash	⊙\odot	⊖\ominus	⊕\oplus
⊘\oslash	⊗\otimes	∥\parallel	⟂\perp
⋔\pitchfork	±\pm	≺\prec	⪷\precapprox
≼\preccurlyeq	≼\preceq	⪹\precnapprox	⋨\precnsim
≾\precsim	∝\propto	⋌\rightthreetimes	≓\risingdotseq
⋊\rtimes	∼\sim	≃\simeq	∕\slash
⌣\smile	⊓\sqcap	⊔\sqcup	⊏\sqsubset
⊏\sqsubset	⊑\sqsubseteq	⊐\sqsupset	⊐\sqsupset
⊒\sqsupseteq	⋆\star	⊂\subset	⊆\subseteq
⫅\subseteqq	⊊\subsetneq	⫋\subsetneqq	≻\succ
⪸\succapprox	≽\succcurlyeq	≽\succeq	⪺\succnapprox
⋩\succnsim	≿\succsim	⊃\supset	⊇\supseteq
⫆\supseteqq	⊋\supsetneq	⫌\supsetneqq	∴\therefore
×\times	⊤\top	◁\triangleleft	⊴\trianglelefteq
≜\triangleq	▷\triangleright	⊵\trianglerighteq	⊎\uplus
⊨\vDash	∝\varpropto	⊲\vartriangleleft	⊳\vartriangleright
⊢\vdash	∨\vee	⊻\veebar	∧\wedge
≀\wr

Símbolos de flecha

⇓\Downarrow	⇐\Leftarrow	⇔\Leftrightarrow	⇚\Lleftarrow
⟸\Longleftarrow	⟺\Longleftrightarrow	⟹\Longrightarrow	↰\Lsh
⇗\Nearrow	⇖\Nwarrow	⇒\Rightarrow	⇛\Rrightarrow
↱\Rsh	⇘\Searrow	⇙\Swarrow	⇑\Uparrow
⇕\Updownarrow	↺\circlearrowleft	↻\circlearrowright	↶\curvearrowleft
↷\curvearrowright	⤎\dashleftarrow	⤏\dashrightarrow	↓\downarrow
⇊\downdownarrows	⇃\downharpoonleft	⇂\downharpoonright	↩\hookleftarrow
↪\hookrightarrow	⇝\leadsto	←\leftarrow	↢\leftarrowtail
↽\leftharpoondown	↼\leftharpoonup	⇇\leftleftarrows	↔\leftrightarrow
⇆\leftrightarrows	⇋\leftrightharpoons	↭\leftrightsquigarrow	↜\leftsquigarrow
⟵\longleftarrow	⟷\longleftrightarrow	⟼\longmapsto	⟶\longrightarrow
↫\looparrowleft	↬\looparrowright	↦\mapsto	⊸\multimap
⇍\nLeftarrow	⇎\nLeftrightarrow	⇏\nRightarrow	↗\nearrow
↚\nleftarrow	↮\nleftrightarrow	↛\nrightarrow	↖\nwarrow
→\rightarrow	↣\rightarrowtail	⇁\rightharpoondown	⇀\rightharpoonup
⇄\rightleftarrows	⇄\rightleftarrows	⇌\rightleftharpoons	⇌\rightleftharpoons
⇉\rightrightarrows	⇉\rightrightarrows	↝\rightsquigarrow	↘\searrow
↙\swarrow	→\to	↞\twoheadleftarrow	↠\twoheadrightarrow
↑\uparrow	↕\updownarrow	↕\updownarrow	↿\upharpoonleft
↾\upharpoonright	⇈\upuparrows

Varios símbolos

ps\$	A\AA	Ⅎ\Finv	⅁\Game
ℑ\Im	¶\P	ℜ\Re	§\S
∠\angle	‵\backprime	★\bigstar	■\blacksquare
▴\blacktriangle	▾\blacktriangledown	⋯\cdots	✓\checkmark
®\circledR	Ⓢ\circledS	♣\clubsuit	∁\complement
©\copyright	⋱\ddots	♢\diamondsuit	ℓ\ell
∅\emptyset	d\eth	∃\exists	♭\flat
∀\forall	ħ\hbar	♡\heartsuit	ℏ\hslash
∭\iiint	∬\iint	i\imath	∞\infty
ȷ\jmath	…\ldots	∡\measuredangle	♮\natural
¬\neg	∄\nexists	∰\oiiint	∂\partial
′\prime	♯\sharp	♠\spadesuit	∢\sphericalangle
ß\ss	▿\triangledown	∅\varnothing	▵\vartriangle
⋮\vdots	℘\wp	¥\yen

Si un símbolo en particular no tiene nombre (como es el caso de muchos de los símbolos más oscuros en las fuentes STIX), también se pueden usar caracteres Unicode:

r'$\u23ce$'

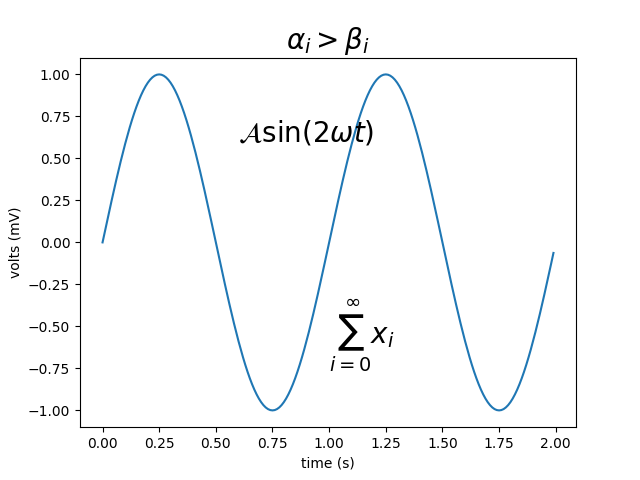
Ejemplo

Aquí hay un ejemplo que ilustra muchas de estas características en contexto.